Задача М903‍‍

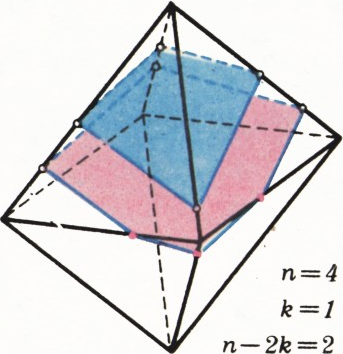
а) Ответ: существует. Покажем, что условию задачи удовлетворяет любой многогранник, из каждой вершины которого выходит чётное число рёбер, например, октаэдр (см. рисунок).

Рассмотрим произвольное сечение такого многогранника, не проходящее через вершины. Очевидно, его можно чуть-чуть пошевелить так, чтобы оно стало непараллельным ни одному из рёбер многогранника, а число его сторон осталось прежним. Будем теперь параллельно перемещать плоскость сечения. Тогда число его сторон будет изменяться только при переходе через вершины, причём каждый раз будет проходиться только одна вершина. Если в ней сходится чётное число $n$‍‍ рёбер и $k$‍‍ из них пересекали плоскость сечения до перехода через эту вершину (а значит, $n-k$‍‍ — после перехода; см. рисунок), то число вершин сечения при этом переходе изменится на $n-2k$‍‍ и, следовательно, его чётность сохранится. А поскольку в конце концов плоскость сечения не будет пересекать ни одно из рёбер, число сторон сечения должно оставаться чётным всё время, за исключением моментов прохождения вершин.

б) Ответ: не существует. Из решения задачи а) следует, что если у всех сечений многогранника, не проходящих через вершины, число сторон имеет одинаковую чётность (в частности, нечётно), то из каждой вершины выходит чётное число рёбер. Но тогда, как было показано там же, число сторон у любого такого сечения должно быть чётно.