Задача М761 / Задачи // Архив журнала «Квант»

Условие задачи (1982, № 9) Задача М761 // Квант. — 1982. — № 9. — Стр. 33—34; 1983. — № 1. — Стр. 45.

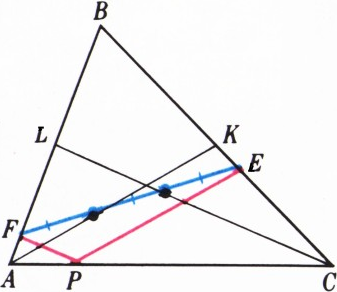
Через произвольную точку $P$‍‍ на стороне $AC$‍‍ треугольника $ABC$‍‍ параллельно его медианам $AK$‍‍ и $CL$‍‍ проведены прямые, пересекающие стороны $BC$‍‍ и $AB$‍‍ в точках $E$‍‍ и $F$‍‍ соответственно (рис. 1). Докажите, что медианы $AK$‍‍ и $CL$‍‍ делят отрезок $EF$‍‍ на три одинаковые части.

Э. Г. Готман

Открыть в номере

Изображения страниц

‍

Скачать PDF

Решение задачи (1983, № 1) Задача М761 // Квант. — 1982. — № 9. — Стр. 33—34; 1983. — № 1. — Стр. 45.

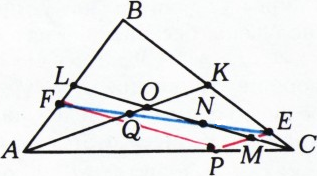
Из подобий $\triangle EMC\sim\triangle OKC$‍‍ и $\triangle PMC\sim\triangle AOC$‍‍ следует, что $\dfrac{|ME|}{|OK|}=\dfrac{|CM|}{|OC|}=\dfrac{|PM|}{|AO|}$‍.‍ Поэтому $\dfrac{|ME|}{|PM|}=\dfrac{|OK|}{|OA|}=\dfrac12$‍.‍ Кроме того, $\triangle NEM\sim\triangle EFP$‍,‍ и поэтому $\dfrac{|NE|}{|EF|}=\dfrac{|ME|}{|PE|}=\dfrac13$‍.‍

Следовательно, $|EN|=\dfrac13|EF|$‍.‍ Так же доказывается, что $|FQ|=\dfrac13|EF|$‍.‍ Поэтому $|FQ|=|QN|=|NE|$‍.‍

А. А. Егоров

Открыть в номере

Метаданные Задача М761 // Квант. — 1982. — № 9. — Стр. 33—34; 1983. — № 1. — Стр. 45.

Предмет

Математика

Условие

Готман Э. Г.

Решение

Егоров А. А.

Номера

1982. — № 9. — Стр. 33—34 [условие]

1983. — № 1. — Стр. 45 [решение]

Описание

Задача М761 // Квант. — 1982. — № 9. — Стр. 33‍—‍34; 1983. — № 1. — Стр. 45.

Ссылка

https://www.kvant.digital/problems/m761/