Задача М693‍‍

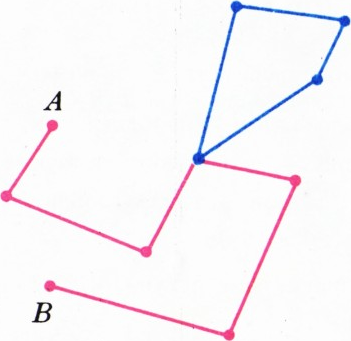
Сопоставим каждому жителю посёлка некоторую точку на плоскости. Те точки, которые соответствуют знакомым между собой жителям, соединим отрезком. Получающаяся картинка называется графом. Выделенные точки называются вершинами графа, а связывающие их отрезки — рёбрами.

Та часть условия задачи, в которой требуется, чтобы новость, сообщённая одному жителю посёлка, в конце концов становилась известной всем его жителям, соответствует тому, что по рёбрам нашего графа можно пройти от любой его вершины до любой другой. Такой граф называют связным. Последовательность рёбер графа, связывающую две его вершины, в которой нет повторяющихся рёбер, называют цепью. Если цепь начинается и кончается в одной и той же вершине, её называют циклом. На рисунке 1 показана цепь, соединяющая вершины $A$‍‍ и $B$‍,‍ а также цикл. Связный граф, не содержащий циклов, называют деревом. Он действительно похож на дерево (см. рис. 2).

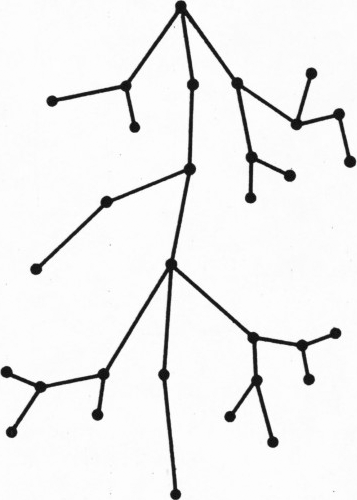
Назовём расстоянием между двумя вершинами графа количество рёбер в самой короткой цепи, соединяющей эти вершины. (Заметим, что если граф является деревом, то любую пару его вершин соединяет лишь одна цепь.)

Введённые понятия позволяют упростить запись решения задачи. В новых терминах формулировка может быть переписана так:

Доказать, что в связанном графе с 1000 вершинами можно указать такое множество из 90 вершин, что для любой вершины графа найдётся вершина из этого множества, расстояние до которой не больше 10.

Пусть $X$‍‍ и $Y$‍‍ — две вершины нашего графа, находящиеся на наибольшем расстоянии. Если это расстояние не больше 10, то расстояние от любой вершины нашего графа до любой другой не больше 10 — в этом случае 90 вершин можно выбрать произвольно.

Заметим, что достаточно решить нашу задачу лишь для случая, когда граф является деревом. Действительно, пусть наш граф — не дерево; тогда он содержит хотя бы один цикл. Если мы выбросим из графа какое-нибудь ребро, принадлежащее этому циклу, цикл исчезнет, а граф останется связным. Поскольку в графе — лишь конечное количество циклов, применив несколько раз эту операцию, мы превратим наш граф в дерево. Множество из 90 вершин полученного дерева, удовлетворяющее условию задачи, очевидно, будет годиться и для первоначального графа, так как прибавление новых рёбер не увеличивает расстояния между вершинами.

Итак, пусть у нас имеется дерево с 1000 вершинами, $X$‍‍ и $Y$‍‍ — две вершины, находящиеся на максимальном расстоянии, которое больше 10. Рассмотрим цепь, соединяющую вершины $X$‍‍ и $Y$‍:‍ $X$‍‍—$A_1$‍‍—$A_2$‍‍—$A_3$‍‍—$\ldots$‍‍—$A_{10}$‍‍—$A_{11}$‍‍—$\ldots$‍‍—$Y$‍.‍ Возьмём точку $A_{10}$‍‍ в качестве первой точки $K_1$‍‍ искомого множества. Если мы сотрём ребро между вершинами $A_{10}$‍‍ и $A_{11}$‍,‍ наше дерево разобьётся на два дерева. Отметим, что часть, содержащая вершину $X$‍,‍ содержит не менее 11 вершин.

Заметим, что расстояние от вершины $A_{10}$‍‍ до каждой из вершин содержащей её части не более 10 (если расстояние от некоторой вершины $M$‍‍ будет больше 10, то расстояние от $M$‍‍ до $Y$‍‍ будет больше расстояния от $X$‍‍ до $Y$‍,‍ что противоречит тому, что вершины $X$‍‍ и $Y$‍‍ находятся на максимальном расстоянии).

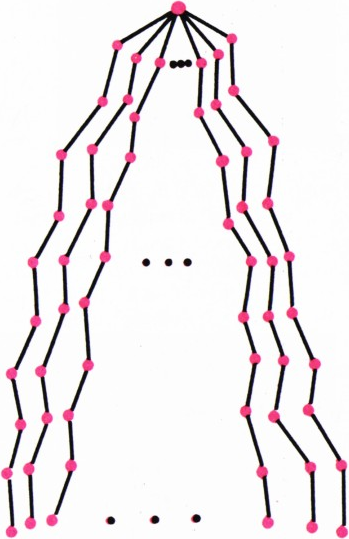
Рассмотрим теперь ту часть графа, которая содержит вершину $Y$‍.‍ Это — дерево, содержащее не более $1000-11=989$‍‍ вершин. Повторим с ним ту же самую операцию. В результате получим ещё одну группу из не менее 11 вершин и среди них — точку $K_2$‍‍ искомого множества, а также дерево, содержащее не больше $1000-2\cdot11=978$‍‍ вершин. После того как мы проделаем эту операцию 89 раз, мы получим 89 групп вершин, расстояние которых до каждой вершины своей группы не превосходит 10. Останется дерево, содержащее не более $1000-89\cdot11=21$‍‍ вершину. Вновь рассмотрим в нём две вершины, находящиеся на максимальном расстоянии, и вновь возьмём в цепи, соединяющей эти вершины, десятую вершину. Очевидно, что эта вершина годится в качестве точки $K_{90}$‍‍ искомого множества. Задача решена.

То, что в связанном графе с 1000 вершинами нельзя выделить нужного множества, состоящего менее чем из 90 вершин, следует из того, что этого нельзя сделать уже для дерева с 991 вершиной, устроенного так: из одной его вершины исходят 90 лучей, на каждом из которых находится по 11 вершин (см. рис. 3).