Задача М927‍‍‍

а) Докажем, что через конечное число операций «типа а» — замены пересекающихся отрезков $AC$‍‍ и $BD$‍‍ на непересекающиеся $AB$‍‍ и $CD$‍‍ — мы придём к конфигурации, в которой уже не будет пересекающихся отрезков.

Рассмотрим сумму $s$‍‍ длин всех отрезков конфигурации. При каждой операции типа a она уменьшается: $$ AB+CD\lt AC+BD\tag{*} $$ (для треугольников $APB$‍‍ и $CPD$‍,‍ где $P$‍‍ — точка пересечения $AC$‍‍ и $BD$‍‍ — рис. 1, выполнены неравенства $AB\lt AP+PB$‍‍ и $CD\lt CP+PD$‍;‍ сложив их, получим (*)).

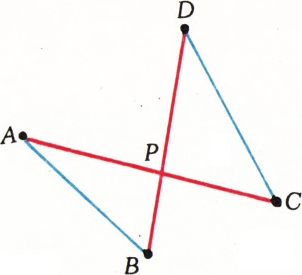
С другой стороны, величина $s$‍‍ может принимать лишь конечное число различных значений, поскольку существует лишь конечное число различных конфигураций из отрезков с вершинами в данных точках. Поэтому через конечное число шагов мы придём к конфигурации, с которой уже нельзя проделать операцию, уменьшающую $s$‍.‍

Это решение даёт очень грубую верхнюю оценку для максимального количества $T_n$‍‍ операций, которое может быть проделано с конфигурацией на $n$‍‍ точках — можно сказать лишь, что оно меньше числа всех конфигураций, т. е. $2^{\frac{\scriptstyle n(n-1)}{\scriptstyle 2}}$‍‍ $\Big(\dfrac{n(n-1)}2$‍‍ — это число различных отрезков с концами в данных $n$‍‍ точках).

Приведём идею другого решения, дающего значительно лучшую оценку. Рассмотрим произвольное разбиение $f$‍‍ данных точек на два непустых множества, каждое из которых лежит целиком по одну сторону от некоторой прямой $l$‍.‍ Таких прямых для данного разбиения, конечно, бесконечно много, но одну из них всегда можно получить, повернув по часовой стрелке прямую, соединяющую две какие-либо точки $A$‍‍ и $B$‍‍ на очень маленький угол вокруг середины отрезка $AB$‍‍ (рис. 2); эту прямую обозначим $l_f$‍.‍ Число прямых $l_f$‍,‍ а значит и число рассматриваемых «выпуклых» разбиений не превосходит числа пар точек $\dfrac{n(n-1)}2$‍.‍

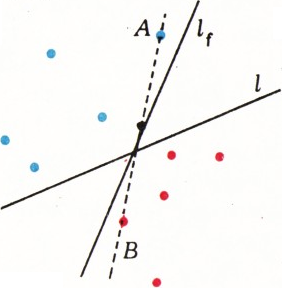
Назовём балансом конфигурации суммарное число $b$‍‍ пересечений её отрезков со всеми прямыми $l_f$‍;‍ ясно, что $0\le b\le\left(\dfrac{n(n-1)}2\right)^2$‍.‍ При операции типа $a$‍‍ число пересечений любой прямой $l_f$‍‍ с отрезками конфигурации не увеличивается, а по крайней мере для одной прямой оно уменьшается на 2. Следовательно, $T_n\le\dfrac{n^2(n-1)^2}8$‍.‍ Интересно было бы получить ещё более точную оценку для $T_n$‍.‍

б) Приведём пример, показывающий, что для операции «типа б» — замены пересекающихся отрезков $AC$‍‍ и $BD$‍‍ на имеющие общий конец $AB$‍‍ и $BC$‍‍ — процесс может «зациклиться» и тем самым продолжаться неограниченно. Расположим 18 точек в вершинах правильного 18-угольника и обозначим через $D(k,l)$‍‍ конфигурацию из 36 отрезков, в которой каждая из 18 точек соединена с $k$‍‍-й и $l$‍‍-й от неё по счёту.

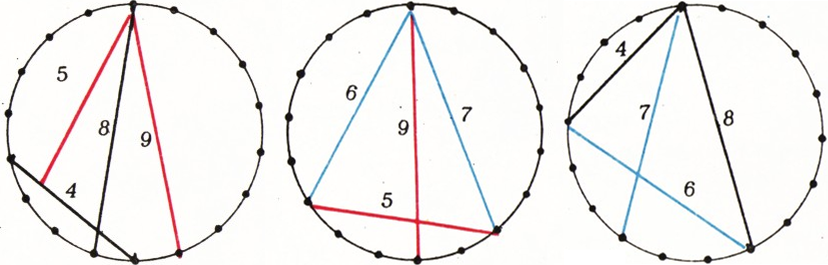
Чтобы пройти за 54 операции путь $D(4,8)\to D(5,9)\to D(6,7)\to D(4,8)$‍‍ (рис. 3), достаточно каждую из операций, изображённых на рисунке 4, проделать по 18 раз (поворачивая картинку каждый раз на $20^\circ$‍).‍

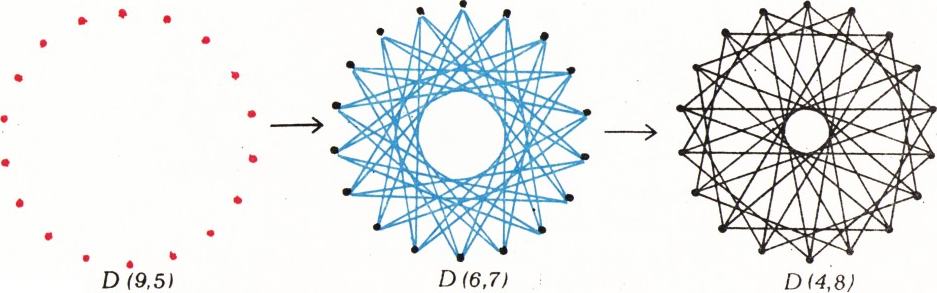
По-видимому, существуют и примеры с существенно меньшим числом точек $n$‍‍ и длиной цикла $T$‍,‍ чем $n=18$‍‍ и $T=54$‍.‍