Задача М838‍‍

Ответ: верно. Доказательство проведём от противного. Пусть точки множества $E_1$‍‍ окрашены синим цветом, множества $E_2$‍‍ — красным. Предположим, что не существует прямоугольного треугольника с одноцветными вершинами, и рассмотрим правильный шестиугольник, вписанный в треугольник $ABC$‍‍ (см. рисунок). Каждые две его противоположные вершины должны быть окрашены по-разному — если, например, противоположные вершины $P$‍‍ и $Q$‍‍ синие, то любая из остальных четырёх вершин должна быть красной, так как образует вместе с $P$‍‍ и $Q$‍‍ прямоугольный треугольник; но тогда любые три из этих красных точек образуют запрещённый одноцветный прямоугольный треугольник.

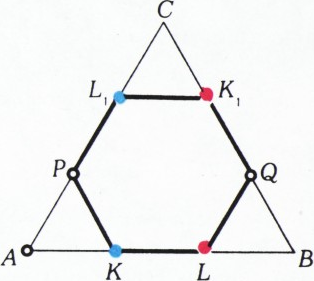
Ясно, что в таком случае найдутся две соседние разноцветные вершины шестиугольника. Либо эти две вершины, либо противоположные им (тоже разноцветные!) лежат на одной из сторон треугольника. Пусть для определённости на стороне $AB$‍‍ лежат синяя вершина $K$‍‍ и красная $L$‍,‍ тогда противоположные им вершины $K_1$‍‍ и $L_1$‍‍ будут красной и синей (см. рисунок). Но тогда, в какой бы цвет ни была окрашена вершина $A$‍,‍ один из прямоугольных треугольников $AKL_1$‍‍ или $ALK_1$‍‍ будет одноцветным. Противоречие.

Это рассуждение доказывает, что даже множество из восьми точек — вершин шестиугольника и любых двух вершин треугольника — нельзя разбить на подмножества без прямоугольных треугольников.