Условие задачи (1983, № 5) Задача М802 // Квант. — 1983. — № 5. — Стр. 42—43; 1983. — № 8. — Стр. 50—51.
На сторонах
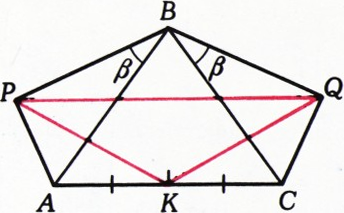
Изображения страниц
Решение задачи (1983, № 8) Задача М802 // Квант. — 1983. — № 5. — Стр. 42—43; 1983. — № 8. — Стр. 50—51.
Ответ:
Эта задача относится к довольно большой группе задач, в которых рассматриваются треугольники или другие многоугольники данной формы, построенные на сторонах другого треугольника или многоугольника. Наверное, самая известная из них — так называемая «задача Наполеона» — доказать, что центры правильных треугольников, построенных на сторонах произвольного треугольника вне его, сами образуют правильный треугольник. Как правило, эти задачи решаются с помощью композиции преобразований плоскости.
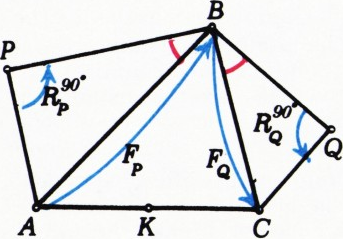
Рассмотрим два преобразования подобия (рис. 1):
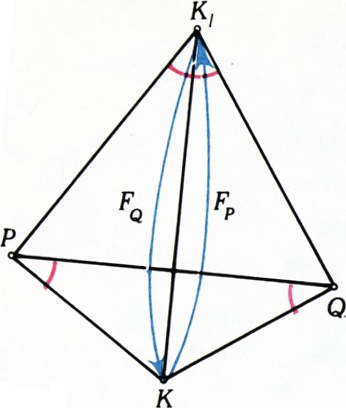
Остаётся доказать, что
$F$ — движение (потому что коэффициент подобия$F$ равен$k\cdot\dfrac1k=1$; - любой луч при движении
$F$ переходит в противоположно направленный (при гомотетии направления лучей сохраняются, при повороте луч поворачивается на угол, равный углу поворота, поэтому общий угол поворота любого луча при преобразовании$F$ равен$90^\circ+90^\circ=180^\circ$); $F(A)=C$ $\Big(F_P(A)=B$ по выбору$F_P$, а$F_Q(B)=C$, потому что$\widehat{BQC}=90^\circ$ и$\dfrac{|QC|}{|QB|}=\dfrac{|PA|}{|PB|}=\dfrac1k\Big)$.
Отсюда вытекает, что
Попробуйте таким же способом решить «задачу Наполеона».



