Задача М760‍‍‍

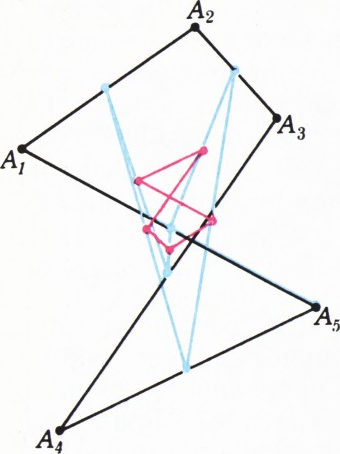
С замкнутой ломаной $A_1A_2\ldots A_m$‍,‍ где $m$‍‍ нечётно, проделывается такая операция: середины её звеньев соединяются $m$‍‍ отрезками через одну (середина $A_1A_2$‍‍ — с серединой $A_3A_4$‍,‍ середина $A_2A_3$‍‍ — с серединой $A_4A_5$‍,‍ $\ldots$‍,‍ $A_{m-1}A_m$‍‍ — с $A_1A_2$‍,‍ а $A_mA_1$‍‍ — с $A_2A_3$‍).‍С полученной ломаной вновь проделывается эта же операция и т. д. Докажите, что из любой $m$‍‍-звенной ломаной:

1. при $m=5$‍‍ — через два шага (рис. 1);
2. при $m=7$‍‍ — через три шага;
3. при любом нечётном $m$‍‍ — через некоторое (зависящее от $m$‍)‍ число шагов

получится ломаная, подобная (даже гомотетичная) первоначальной.