Условие задачи (1981, № 3) Задача М673 // Квант. — 1981. — № 3. — Стр. 24; 1981. — № 11. — Стр. 24.
На плоскости в вершинах треугольника лежат три шайбы
- Покажите, как после пяти ударов шайба
$C$ может вернуться на своё место, а шайбы$A$ и$B$ поменяться местами. - Могут ли все три шайбы
$A$, $B$, $C$ вернуться на свои прежние места после 25 ударов?
Изображения страниц
Решение задачи (1981, № 11) Задача М673 // Квант. — 1981. — № 3. — Стр. 24; 1981. — № 11. — Стр. 24.
а) Нетрудно сообразить, что если по шайбе
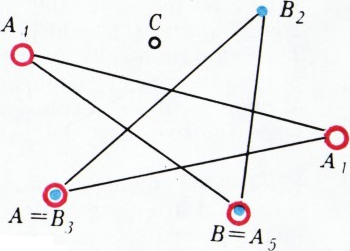
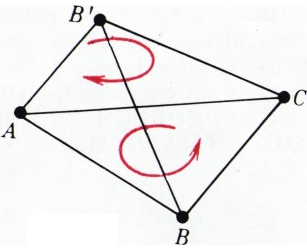
б) Ответ: не могут. Для доказательства проследим за ориентацией треугольника

