Условие задачи (1980, № 12) Задача М658 // Квант. — 1980. — № 12. — Стр. 22—23; 1981. — № 8. — Стр. 41.
В квадрате со стороной 1 проведено конечное число отрезков, параллельных его сторонам. Отрезки могут пересекать друг друга. Сумма длин проведённых отрезков равна 18. Докажите, что среди частей, на которые квадрат разбивается этими отрезками, найдётся такая, площадь которой не меньше 0,01.
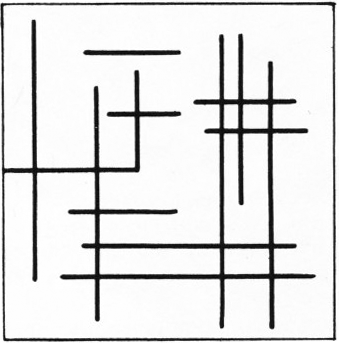
Изображения страниц
Решение задачи (1981, № 8) Задача М658 // Квант. — 1980. — № 12. — Стр. 22—23; 1981. — № 8. — Стр. 41.
Сумма длин границ всех частей, на которые квадрат разбит отрезками, равна
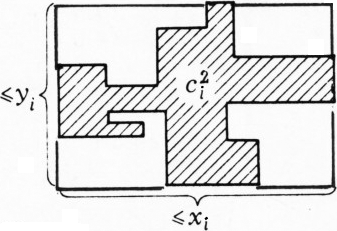
Если


