Задача М602 / Задачи // Архив журнала «Квант»

Условие задачи (1980, № 1) Задача М602 // Квант. — 1980. — № 1. — Стр. 31; 1980. — № 11. — Стр. 27—28.

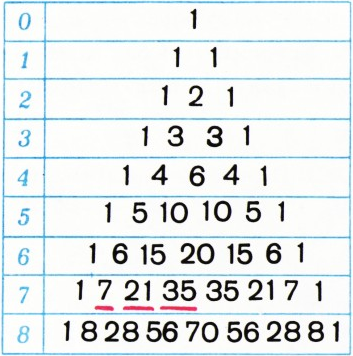
Рис. 1. В <nowrap>{literal}$n$‍{/literal}</nowrap>‍-й строчке <nowrap>{literal}$k$‍{/literal}</nowrap>‍-е по порядку число равно <nowrap>{literal}$C n^k=\dfrac{ldelim}n(n-1)\ldots(n-k+1){rdelim}{ldelim}1\cdot2\cdot\ldots\cdot k{rdelim}$‍{/literal}</nowrap>‍ — Рис. 1. В $n$‍‍-й строчке $k$‍‍-е по порядку число равно $C_n^k=\dfrac{n(n-1)\ldots(n-k+1)}{1\cdot2\cdot\ldots\cdot k}$‍‍

В треугольнике Паскаля, начало которого изображено на рисунке 1 (каждое «внутреннее» число равно сумме двух стоящих над ним), в седьмой строке встречаются подряд три числа, образующие арифметическую прогрессию.

В какой следующей строке случится такое же событие?
Докажите, что оно произойдёт в бесконечном количестве строк, и постарайтесь указать все номера таких строк.

А. Аврамов

Открыть в номере

Изображения страниц

‍

Скачать PDF

Решение задачи (1980, № 11) Задача М602 // Квант. — 1980. — № 1. — Стр. 31; 1980. — № 11. — Стр. 27—28.

Текстовое представление решения задачи находится в процессе подготовки. С графическим представлением можно ознакомиться в опубликованном номере

Открыть в номере

Метаданные Задача М602 // Квант. — 1980. — № 1. — Стр. 31; 1980. — № 11. — Стр. 27—28.

Предмет

Математика

Условие

Аврамов А.

Решение

Аврамов А.

Номера

1980. — № 1. — Стр. 31 [условие]

1980. — № 11. — Стр. 27—28 [решение]

Описание

Задача М602 // Квант. — 1980. — № 1. — Стр. 31; 1980. — № 11. — Стр. 27‍—‍28.

Ссылка

https://www.kvant.digital/problems/m602/