Задача М588‍‍

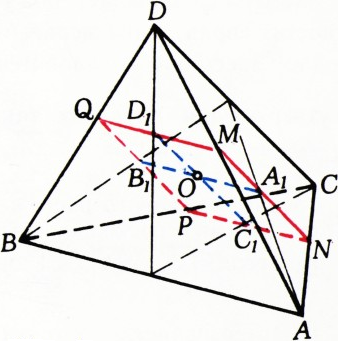
а) Проведём через точку $O$‍‍ внутри тетраэдра $ABCD$‍‍ отрезки $[A_1B_1]\parallel[AB]$‍‍ и $[C_1D_1]\parallel[CD]$‍,‍ где $A_1\in(ACD)$‍,‍ $B_1\in(BCD)$‍,‍ $C_1\in(ABC)$‍,‍ $D_1\in(ABD)$‍‍ (рис. 1). Эти отрезки определяют плоскость, пересекающую грани $ABC$‍‍ и $ABD$‍‍ по прямым $PN$‍‍ и $MQ$‍,‍ параллельным $(AB)$‍,‍ а грани $ACD$‍‍ и $BCD$‍‍ — по прямым $MN$‍‍ и $PQ$‍,‍ параллельным $(CD)$‍.‍ Значит, четырёхугольник $MNPQ$‍‍ — параллелограмм. Имеем $$ \frac{|A_1B_1|}{|AB|}=\frac{|MQ|}{|AB|}=\frac{|DM|}{|AD|},\quad \frac{|C_1D_1|}{|CD|}=\frac{|MN|}{|CD|}=\frac{|AM|}{|AD|}. $$ Отсюда $$ \frac{|A_1B_1|}{|AB|}+\frac{|C_1D_1|}{|CD|}=\frac{|DM|}{|AD|}+\frac{|AM|}{|AD|}=\frac{|DM|+|AM|}{|AD|}=1. $$

Итак, сумма отношений длин двух проведённых отрезков к длинам параллельных им скрещивающихся рёбер тетраэдра равна единице. Следовательно, сумма всех шести отношений равна трём.

б) Докажем, что если через точку, взятую внутри произвольного треугольника, параллельно его сторонам проведены отрезки с концами на сторонах треугольника, то сумма трёх отношений длин этих отрезков к длинам параллельных им сторон равна двум.

Пусть $O$‍‍ — точка внутри $\triangle ABC$‍,‍ $A_1A_2$‍,‍ $B_1B_2$‍,‍ $C_1C_2$‍‍ — отрезки, параллельные сторонам треугольника (рис. 2). Из подобия треугольников $ABC$‍,‍ $C_1CC_2$‍‍ и $A_1AA_2$‍‍ получаем (обозначения см. на рисунке 2) $$ \frac{|C_1C_2|}{|AB|}=\frac{|CC_1|}{|AC|}=\frac{x+y}{|AC|},\quad \frac{|A_1A_2|}{|BC|}=\frac{|AA_2|}{|AC|}=\frac{z+y}{|AC|}. $$ Кроме того, $$ \frac{|B_1B_2|}{|AC|}=\frac{x+z}{|AC|} $$ (см. рис. 2). 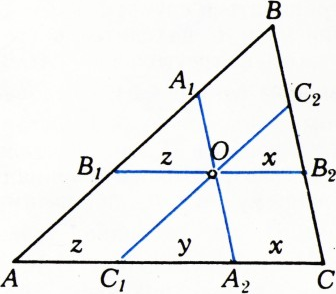Поэтому $$ \frac{|A_1A_2|}{|BC|}+\frac{|B_1B_2|}{|AC|}+\frac{|C_1C_2|}{|AB|}=\frac{z+y}{|AC|}+\frac{x+z}{|AC|}+\frac{x+y}{|AC|}=\frac{2(x+y+z)}{|AC|}=2, $$ что и требовалось доказать.