Задача М577‍‍

Ответ: $2n$‍‍ фишек при $n$‍‍ чётном (в частности, 16 при $n=8$‍),‍ и $2n+1$‍‍ — при $n$‍‍ нечётном.

Одна из возможных расстановок фишек показана на рисунках 1 и 2. Докажем, что меньшим количеством фишек обойтись не удастся.

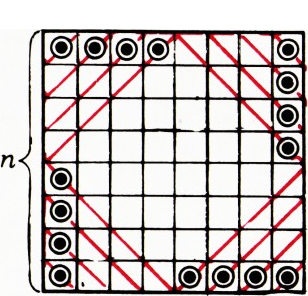
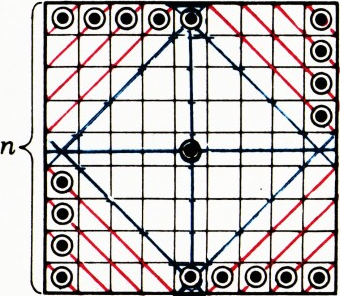
Начнём с более трудного случая нечётного $n$‍‍ (рис. 2). Очевидно, на каждом из красных отрезков, параллельных диагоналям и расположенных вне голубого квадрата, должно стоять по фишке; этих отрезков $2n-2$‍.‍ На каждом из голубых отрезков тоже должна стоять фишка. Покажем, что для этого придётся добавить ещё не менее трёх фишек; действительно, чтобы двумя фишками «закрыть» все четыре стороны голубого квадрата, их пришлось бы поставить в противоположные вершины этого квадрата, но тогда осталась бы свободной одна диагональ квадрата.

Случай чётного $n$‍‍ теперь очевиден: здесь просто указывается $2n$‍‍ непересекающихся отрезков, параллельных диагоналям (рис. 1).

Предлагаем читателям выяснить, сколько существует различных расстановок наименьшего количества фишек, удовлетворяющих условию (для разных $n$‍),‍ и обобщить задачу на случай прямоугольных досок размером $m\times n$‍.‍ Было бы также интересно исследовать различные пространственные аналоги этой задачи (возникающие здесь вопросы, видимо, очень трудны; см. статью «Расстановка кубиков»‍ — «Квант», 1972, № 4).