Задача М541‍‍

а) Подсчитаем число пар друзей. Поскольку каждый имеет трёх друзей, т. е. входит в 3 такие пары, то общее число пар равно $\dfrac{3N}2$‍.‍ Отсюда следует, что $N$‍‍ чётно.

Если изображать людей точками — вершинами, а друзей соединять отрезками — рёбрами, то конфигурация, удовлетворяющая условию задачи, будет однородным графом степени 3 (от каждой вершины отходит 3 ребра). На языке графов наше решение можно записать так: поскольку у каждого из $M$‍‍ рёбер графа два конца и каждая из $N$‍‍ вершин служит концом трёх рёбер, $2M=3N$‍,‍ откуда $M=\dfrac{3N}2$‍.‍

б) Ответ. Не всегда. Простейший пример, который привели почти все читатели, правильно решившие задачу, содержит 16 вершин и, стало быть, 24 ребра (рис. 2). Если выбрать пару $OA_1$‍,‍ то пятёрки, содержащие $A_2$‍‍ и $A_3$‍,‍ уже нельзя разбить на пары. Как отметил десятиклассник В. Губа из Вологды, такие примеры существуют при всех чётных $N\ge16$‍.‍

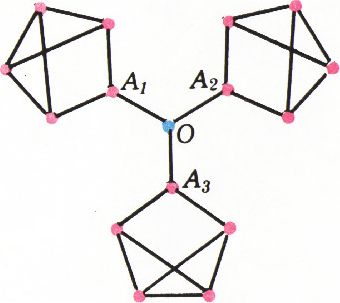
Во всех контрпримерах, приведённых читателями, на графе имеется перешеек — ребро, после выбрасывания которого граф распадается на два куска (в нашем примере три перешейка: $OA_1$‍,‍ $OA_2$‍‍ и $OA_3$‍).‍ Это не случайно. Можно доказать — предлагаем это как задачу читателям, — что в однородном графе степени 3 без перешейков всегда существует совершенное паросочетание , т. е. множество рёбер, содержащих все вершины графа и не имеющих общих вершин. (См., например, главу 18 книги К. Бержа «Теория графов и её применения» (М., ИЛ, 1962).)

Задачи о паросочетаниях — достаточно продвинутый раздел теории графов. О некоторых из этих задач рассказывалось в «Кванте» (1970, № 4, с. 14‍; 1974, № 11, с. 23‍).