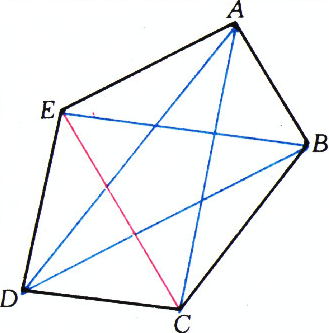
Пусть $F = [AD] \cap [BE]$, $G = [AC] \cap [BE]$ и $K = [BD] \cap [AC]$ (см. рис. 2).
Рисунок номер 2
Из подобия треугольников $AEF$ и $BCD$ следует, что $\dfrac{|AF|}{|EF|}=\dfrac{|BC|}{|CD|}$. Следовательно, $\dfrac{|AF|+ |BC|}{|EF|+|CD|}=\dfrac{|BC|}{|CD|}$ и $\dfrac{|AD|}{|BE|}=\dfrac{|BC|}{|CD|}$, поскольку $|BC|=|DF|$, $|BF|=|CD|$, т. е.
$$
\dfrac{|BC|}{|AD|}=\dfrac{|CD|}{|BE|}. \tag{1}
$$
Аналогично, из подобия треугольников $BKC$ и $AED$ получаем, что $$
\dfrac{|AE|}{|BD|}=\dfrac{|DE|}{|AC|}. \tag{2}
$$
Наконец, из подобия треугольников $BKG$ и $AGE$ $\dfrac{|BG|}{|BK|}=\dfrac{|CD|}{|AE|}$, откуда $\dfrac{|BE|}{|BD|}=\dfrac{|CD|}{|AE|}$, или $$
\dfrac{|CD|}{|BE|}=\dfrac{|AE|}{|BD|}. \tag{3}
$$
Из соотношений (1) — (3) следует, что $$
\dfrac{|BC|}{|AD|}=\dfrac{|CD|}{|BE|}=\dfrac{|AE|}{|BD|}=\dfrac{|DE|}{|AC|}=\lambda. \tag{4}
$$
Далее:
$$\begin{gather*}
\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EA}+\overrightarrow{AB}=\overrightarrow{0},\\
\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{DB}+\overrightarrow{CA}+\overrightarrow{EC}=\overrightarrow{0},
\end{gather*}$$
и $\overrightarrow{BC}=\lambda\overrightarrow{AD}$, $\overrightarrow{CD}=\lambda\overrightarrow{BE}$, $\overrightarrow{DE}=\lambda\overrightarrow{CA}$, $\overrightarrow{EA}=\lambda\overrightarrow{DB}$. Поэтому
$$
\overrightarrow{0}=\lambda(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CA}+\overrightarrow{DB})+\overrightarrow{AB}=-\lambda\overrightarrow{EC}+\overrightarrow{AB},
$$
откуда $\overrightarrow{AB}=\lambda\overrightarrow{EC}$, что и означает параллельность стороны $AB$ диагонали $EC$.
Более короткое решение получается с помощью косоугольной системы координат. Пусть точки $D$, $C$ и $E$ имеют координаты $D\, (0; 0)$, $C\, (1; 0)$, $E\, (0; 1)$ (рис. 2). Тогда $A$ и $B$ имеют координаты $(1; a)$ и $(b; 1)$, так как $(CD) \parallel (BE)$, $(DE) \parallel (AC)$. Условия параллельности $(AE) \parallel (BD)$ и $(BC) \parallel (AD)$ записываются так:
$$
\dfrac{a-1}{1-0}=\dfrac{1-0}{b-0} \quad \text{и} \quad \dfrac{1-0}{b-1}=\dfrac{a-0}{1-0},
$$
т. е. $b(a-1)=1$, $a(b-1)=1$, откуда $a=b$ и $\dfrac{a-1}{1-b}=\dfrac{1-0}{0-1}$, т. е. $(AB) \parallel (EC)$.
Заметим, что пятиугольник $ABCDE$, о котором идёт речь в этой задаче, можно аффинным преобразованием (или просто перекосом) превратить в правильный.