Задача М377‍‍

Эта задача — на построение циркулем и линейкой; публикуя её, мы надеялись получить именно такое, чисто геометрическое решение. Многие же читатели искали точку $D$‍,‍ составляя уравнения и проводя довольно громоздкие вычисления.

Предположим, что искомая точка $D$‍‍ найдена, т. е. что $P_{\triangle ABD}=|BC|$‍‍ (см. рис. 1). Тогда если от точки $D$‍‍ отложить отрезок $DK$‍,‍ равный по длине отрезку $BD$‍,‍ то длина отрезка $AK$‍‍ будет равна разности длин сторон $BC$‍‍ и $AB$‍‍ треугольника $ABC$‍.‍

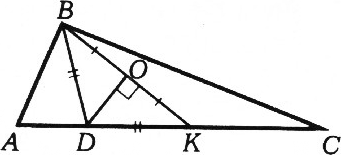
Из этого замечания ясно, как решать задачу. На стороне $AC$‍‍ от точки $A$‍‍ отложим отрезок $AK$‍:‍ $|AK|=|BC|-|AB|$‍,‍ и соединим точку $K$‍‍ с вершиной $B$‍.‍ Из середины $O$‍‍ отрезка $BK$‍‍ восставим перпендикуляр; точка пересечения этого перпендикуляра со стороной $AC$‍‍ и будет искомой $D$‍‍ ($OD\perp BK$‍‍ и $O$‍‍ — середина $BK$‍;‍ следовательно, $|BD|=|DK|.$‍‍

Осталось выяснить, всегда ли задача имеет решение. В треугольнике $ABD$‍:‍ $|AD|+|BD|\gt|AB|$‍,‍ т. е. $P_{\triangle ABD}=|AD|+|BD|+|AB|\gt2|AB|$‍.‍ Следовательно, задача имеет решение, если $|BC|\gt2|AB|$‍.‍