Условие задачи (1970, № 1) Задача М3 // Квант. — 1970. — № 1. — Стр. 52—53; 1970. — № 7. — Стр. 54—55; 1970. — № 8. — Стр. 42—46.
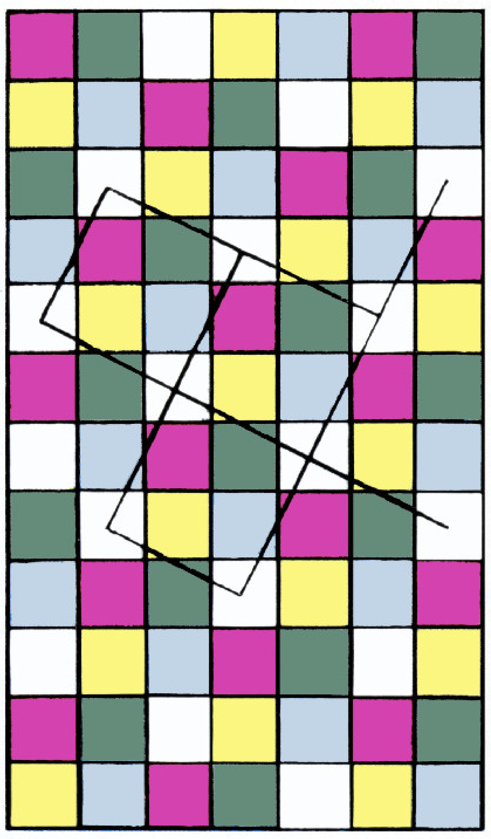
На рисунке 1 плоскость покрыта квадратами пяти цветов. Центры квадратов одного и того же цвета расположены в вершинах квадратной сетки. При каком числе цветов возможно аналогичное заполнение плоскости?

На рисунке 2 плоскость покрыта шестиугольниками семи цветов так, что центры шестиугольников одного и того же цвета образуют вершины решетки из одинаковых правильных треугольников. При каком числе цветов возможно аналогичное построение?
Примечание. В первой задаче число цветов может равняться единице (все квадраты одного цвета) и двум (как на шахматной доске). Во второй задаче вы без труда найдете решения с одним цветом и с тремя цветами. Желательно дать полное решение задач, т. е. описать все раскраски, удовлетворяющие указанным условиям. Присылайте, однако, и неполные решения, если они покажутся вам интересными. Подумайте, например, существует ли во второй задаче решение с тринадцатью цветами?
Изображения страниц
Решение задачи (1970, № 7) Задача М3 // Квант. — 1970. — № 1. — Стр. 52—53; 1970. — № 7. — Стр. 54—55; 1970. — № 8. — Стр. 42—46.
Полных решений этой задачи мы пока не получили.
Ученик 6-го класса Сергей Елисеев (Москва) прислал нам раскраску шестиугольной сетки тринадцатью цветами, которую мы воспроизводим, насколько это позволяют полиграфические возможности, на рисунке 8; он утверждает (без объяснений), что ответ в общем случае такой:
В задаче a) требуемая раскраска возможна, если количество цветов равно сумме двух квадратов целых чисел: $$ \begin{alignat*}{3} 1&=0^2+1^2;&\quad 2&=1^2+1^2;&\quad 4&=0^2+2^2;\\ 5&=1^2+2^2;&\quad 8&=2^2+2^2;&\quad 9&=0^2+3^2;\\ 10&=1^2+3^2;&\quad13&=2^2+3^2;&\quad16&=0^2+4^2 \end{alignat*} $$ и т. д.
В задаче б) решение возможно при количестве цветов, равном сумме двух
чисел из последовательности 0, 1, 3, 6, 10, 15,
Попробуйте выяснить, правильны ли эти ответы? К этому вопросу мы вернёмся позже, а пока обратим внимание на одну тонкость в формулировке задачи (первым её заметил читатель В. Гутенмахер из Москвы).
Начнём с задачи a). В ней требуется найти раскраски, при которых «центры
квадратов одного и того же цвета расположены в вершинах квадратной сетки».
Но в условии не сказано, что для разных цветов эта «большая» квадратная
сетка должна быть одинаковой. Посмотрите на рисунок 9. Здесь тоже
квадраты каждого из трёх цветов образуют сетку, но для красного цвета «шаг»
(сторона квадрата) сетки равен


Но если понимать условие задачи буквально — а на письменном экзамене или на олимпиаде именно так и следует поступать, — то раскраска рисунка 9 удовлетворяет условию задачи. При подобном понимании ответ в задаче а)
будет такой: при любом числе цветов. Действительно, из любой
раскраски с
При таком понимании и задача б) становится совсем простой.
Ответ. При любом числе цветов, большем 2. Действительно, раскраска двумя цветами невозможна, поскольку, если из трёх шестиугольников, каждые два из которых имеют общую сторону, два покрашены в один цвет, то и все шестиугольники должны быть раскрашены этим цветом. Раскраски с 3 и 4 цветами находятся легко, а дальше нетрудно, раскрашивая белые шестиугольники в три цвета, увеличить число цветов на 2, затем ещё на 2 и т. д.
Разумеется, таким способом можно получить много
разнообразных раскрасок. Имея любую раскраску А
Итак, в такой «буквальной» формулировке задача оказывается совсем простой. Однако, автор задачи, а также большинство читателей журнала, приславших нам решения, понимали условие иначе; а именно, они хотели найти такие раскраски, при которых решётки, соответствующие разным цветам, одинаковы и получаются друг из друга параллельным сдвигом (как на рисунках, сопровождающих условие задачи, и на рис. 8). Решение задачи М3 с таким уточнением мы приведём в следующем номере.
Решение задачи (1970, № 8) Задача М3 // Квант. — 1970. — № 1. — Стр. 52—53; 1970. — № 7. — Стр. 54—55; 1970. — № 8. — Стр. 42—46.
Теперь будем считать правильным только такое заполнение плоскости квадратами (или шестиугольниками), при котором сетка, соответствующая какому-то одному цвету, имеет такие же размеры и направления сторон квадратов (или треугольников), как и сетка, соответствующая любому другому цвету. Иначе говоря, все сетки должны получаться друг из друга параллельным сдвигом. Разумеется, разные сетки не могут быть закрашены одним цветом. Решение задачи для обоих случаев (квадраты и шестиугольники) аналогично, и мы рассмотрим оба случая сразу.


I. Докажем сначала, что если плоскость заполнена указанным образом,
то число цветов равно
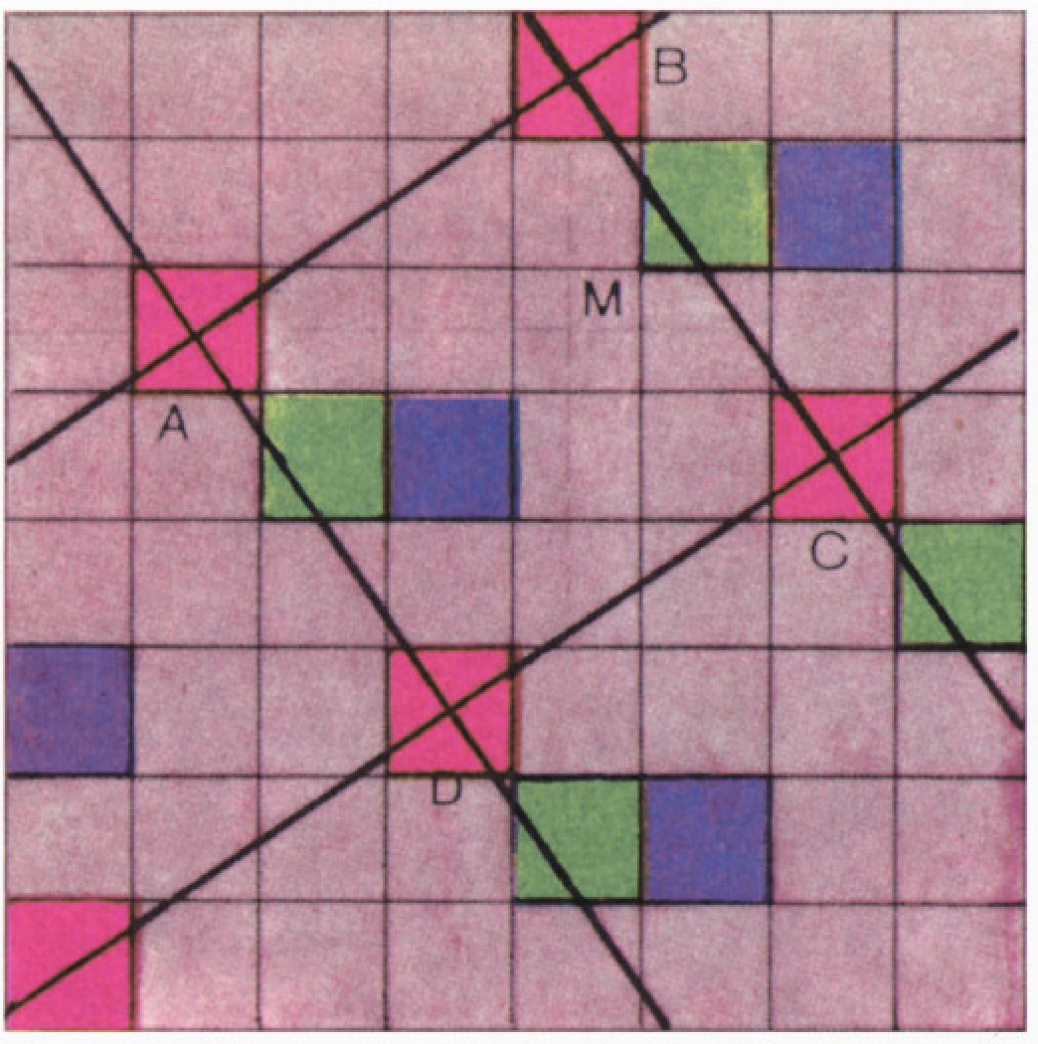
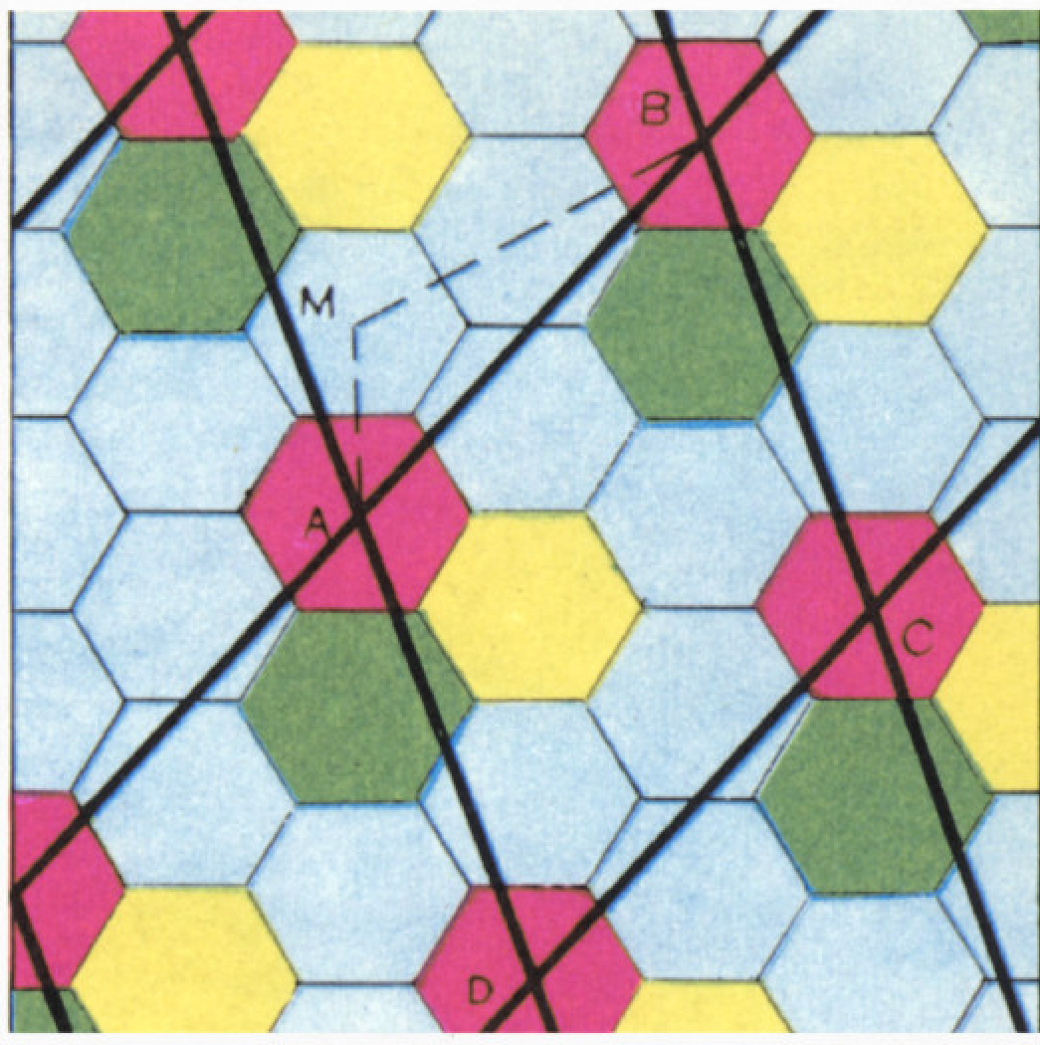
Примем за единицу длины расстояние между центрами двух соседних квадратов или шестиугольников.
Начертим жирными чёрными линиями сетку, проходящую через центры квадратов или шестиугольников одного цвета, скажем, красного (рис. 2, 3). В случае шестиугольников мы проведём линии только двух направлений, так что сетка будет состоять не из правильных треугольников, а из ромбов.
Пусть
В случае квадрата проведём через точки
В случае ромба проведём через точки
Мы докажем, что число цветов, участвующих в раскраске, равно отношению
площади
в случае квадратов
в случае шестиугольников
(так как площадь одного шестиугольника равна
Это сразу следует из следующей леммы.
Основная лемма. Часть
Доказательство леммы несложно, и мы предлагаем читателю провести
его самостоятельно. Заметим только, что раскраска всех квадратов (ромбов)
жирной сетки одинакова, т. е. если вырезать квадрат (ромб)
Существует другой способ изложить это доказательство, более
красивый, но требующий некоторой работы воображения. Ограничимся сначала
случаем квадратной сетки. Вырежем из плоскости квадрат
В случае шестиугольников мы придём к аналогичному
результату, если таким же образом склеим прямоугольник, имеющий одну
сторону, общую с ромбом
Можно заполнить плоскость и другими равными фигурами, в которых площади, закрашенные разными цветами, равны. Например, в решении
задачи (a), присланном из Киева (пер. Белинского, 8, кв. 32, фамилия
автора не указана), предлагается заполнить плоскость фигурами, составленными
из двух квадратов со сторонами

Рис. 4. Плоскость заполнена одинаковыми фигурами площади 13 каждая. Попробуйте найти «элементарный» кусок заполненной таким образом плоскости и склеить из него тор, как мы это сделали с квадратом.
Указание. Надо выбрать 13 фигур, из них сложить многоугольник, который не будет квадратом, но тем не менее легко склеится в тор. Делать это надо с листом клетчатой бумаги.
II. Теперь пусть нам дано число
Заполним плоскость равными квадратами или правильными шестиугольниками и начнём их раскрашивать следующим образом.
Закрасим один из них красным. Отсчитаем от него
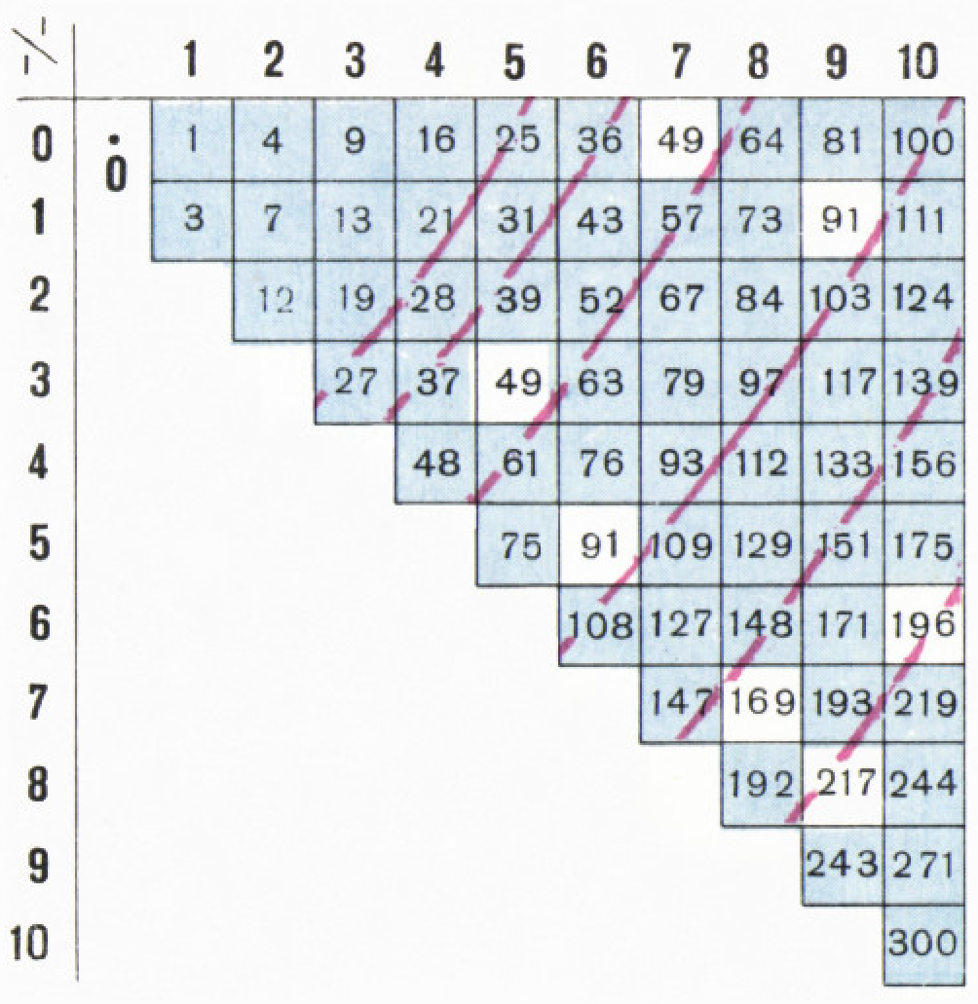
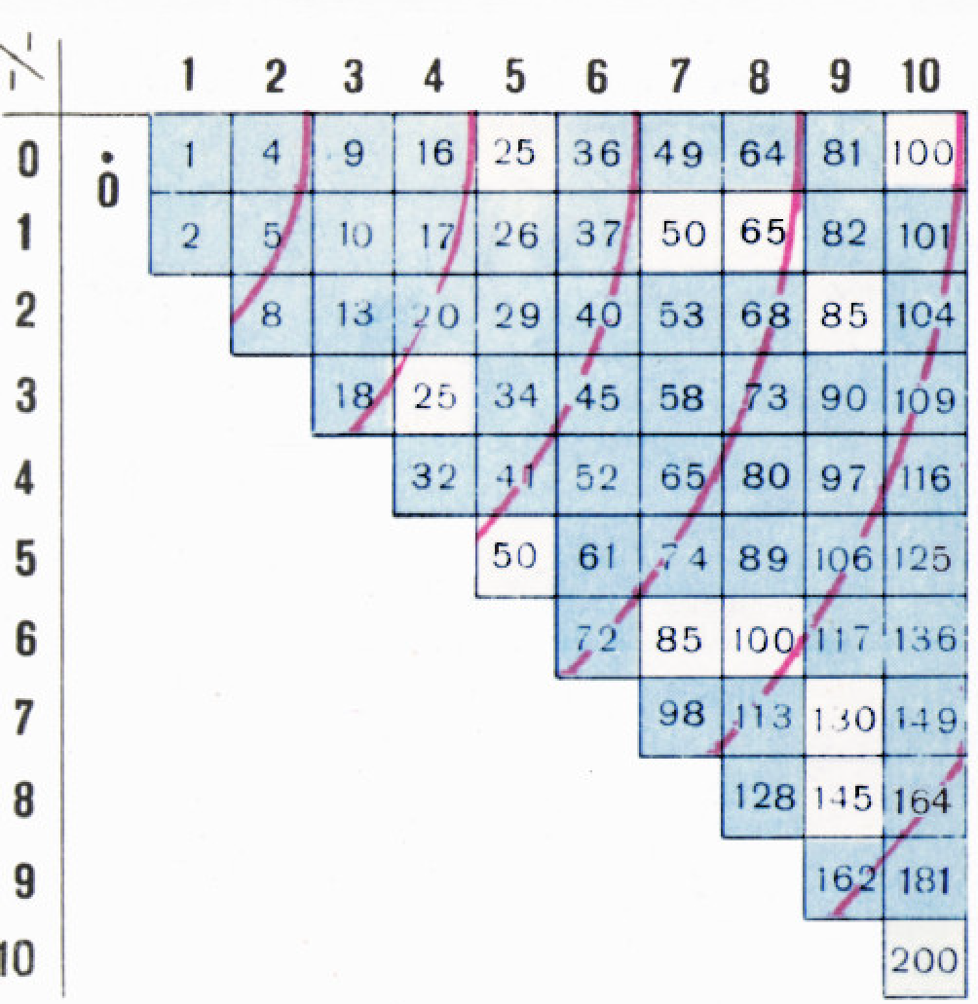
III. Какие же натуральные числа представимы в виде
Числа ниже диагонали повторяют уже написанные, и их писать не нужно. Некоторые числа входят в таблицу дважды; соответствующие клетки выделены. Это значит, что при таком числе цветов имеются два существенно различных способа заполнения плоскости. Теперь уже легко начать выписывать эти числа в порядке возрастания.
Первая таблица: 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 18, 20, 25, 26,
Вторая таблица: 1, 3, 4, 7, 9, 12, 13, 16, 19, 21, 25, 27, 28,
Пусть мы уже выписали эти числа до какого-то места и ищем следующее по величине число.
Красные линии, проведённые на первой таблице, помогают это сделать. Чтобы объяснить, как они проведены, заметим, что в первой таблице
каждое число равно квадрату расстояния от центра той клетки, в которой оно стоит до точки 0 в левом верхнем углу (за единицу длины принимаем сторону
клетки). Поэтому, если провести несколько окружностей с центром 0, то они разобьют наши числа (то есть центры клеток, в которых они стоят) на группы
в порядке возрастания. Если попытаться провести от руки аналогичные линии во второй таблице, то может показаться, что они прямые. Но это, конечно, не так. На самом деле это графики соотношений вида
$$
k^2+kl+l^2=c=\text{const}
$$
в системе координат с началом 0 и осями, идущими: ось
В определённом смысле мы получили ответ, но, быть может, его можно
упростить. Например, если в какой-то другой задаче мы получим ответ:
все числа вида
Проведём в первой таблице красную окружность с центром 0 радиуса
Отсюда среди первых








