Задача М1407‍‍

Ответ: а) 16; $\left[\dfrac{3n+1}2\right]+1$‍‍ для любого $n\gt1$‍.‍

Назовём $n$‍‍ мужчин, стоящих в центре фотографий, взрослыми, остальных (среди всех $m$‍‍ изображённых на фотографиях мужчин) — юными. Отметим на координатной плоскости возможные пары $(n,m)$‍,‍ соответствующие различным наборам фотографий.

Каждый набор изображается как генеалогическое дерево (или «лес» из нескольких таких деревьев): верхний этаж — те, кто не имеет отцов (среди взрослых), предпоследний этаж — их дети, ниже — дети их детей и т. д., вплоть до «нулевого этажа» (где нет ни одного взрослого). Деревья (и леса), которые получаются из набора фотографий, назовём допустимыми.

Деревьям всего из двух этажей (первого и нулевого — см. рис. 1) соответствуют пары $n=1$‍,‍ $m=3$‍;‍ $n=2$‍,‍ $m=4$‍‍ и вообще $n=k$‍,‍ $m=2k$‍‍ (а лесу из нескольких тaких деревьев соответствуют пары, получаемые как суммы векторов $(1,3)$‍,‍ $(2,4)$‍,‍ $(k,2k)$‍).‍

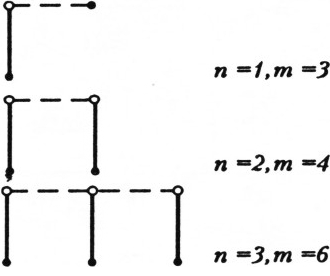
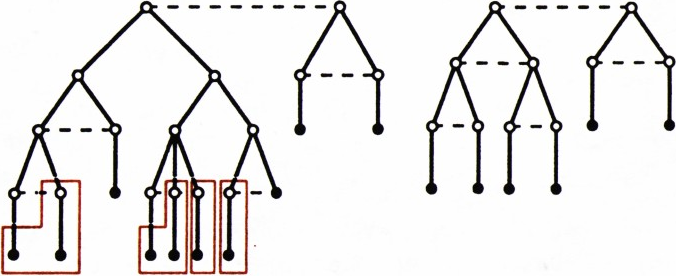
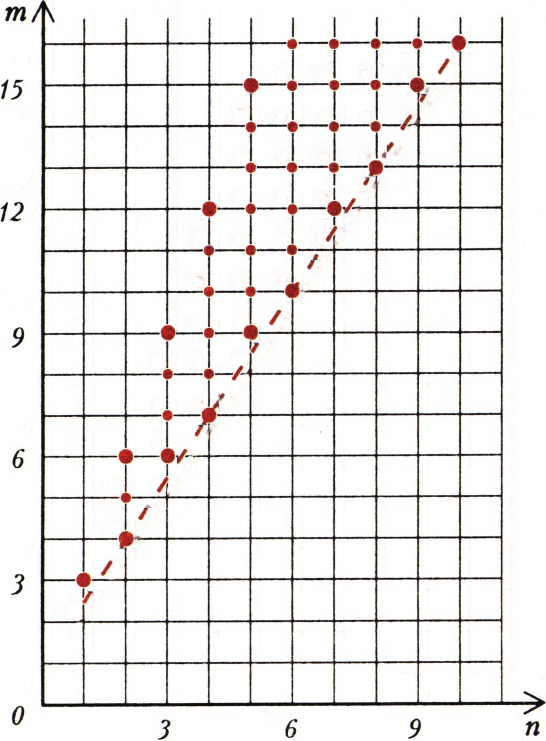
В любом допустимом дереве с бо́льшим числом этажей можно произвести такую операцию: убрать из нижних двух этажей З из 4 людей — двух братьев и их детей, уменьшив число фотографий на 2 (заменив четвёртого — взрослого на юношу), либо убрать 2 людей — отца и сына, уменьшив число фотографий на 1 (рис. 2); такими операциями можно постепенно прийти к дереву всего из двух этажей — это означает, что все отмеченные точки $(n,m)$‍‍ получаются из векторов $(1,3)$‍,‍ $(2,4)$‍‍ прибавлением нескольких векторов $(2,3)$‍‍ и $(1,2)$‍;‍ верно и обратное: все такие суммы векторов дают отмеченные точки — очевидно, что можно соответствующим образом достраивать снизу допустимое дерево.

Мы получили полное описание множества отмеченных точек $(n,m)$‍‍ — на рисунке 3 они выделены цветом. Чтобы ответить на вопросы, заданные в условии, достаточно заметить, что для каждого $n\gt2$‍‍ отмеченная точка $(m,n)$‍‍ с наименьшим $m$‍‍ — точка, лежащая не ниже пунктирной прямой на рисунке 3; при чётном $n$‍‍ это $m=\dfrac{3n}2+1$‍,‍ при нечётном $n$‍‍ это $m=\dfrac{3n+1}2+1$‍.‍ Можно записать ответ в виде единой формулы, как это сделано выше.