Задача М1175‍‍‍

Докажем общее утверждение: при любом расположении выпуклых многоугольников на плоскости один из них можно выдвинуть (сколь угодно далеко по некоторому направлению $d$‍),‍ не задевая остальных. Такой многоугольник найдётся для каждого направления $d$‍.‍

Рассмотрим «проекции» многоугольников на прямую $l$‍,‍ перпендикулярную направлению $d$‍,‍ причём при изображении проекций будем указывать, какой из многоугольников расположен выше ($d$‍‍ мы считаем направлением «вверх», рис. 1); здесь существенна выпуклость многоугольников.

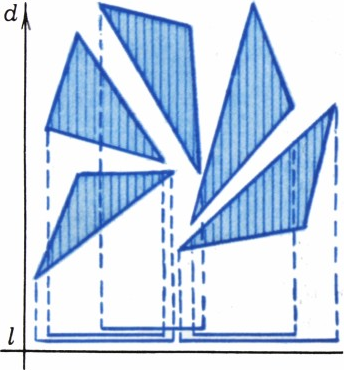
Теперь достаточно доказать следующее утверждение — лемму о коврах: если отрезок-«коридор» покрыт несколькими отрезками-«коврами», то обязательно найдётся ковёр, никакая часть которого не покрыта другим — верхний ковёр.

Очевидно, мы можем считать, что нет ковра, у которого имеется два открытых участка, разделённых закрытым: иначе мы могли бы рассмотреть лишь те ковры, которые лежат сверху на этом закрытом участке, и среди них искать верхний ковёр. Точно так же можно исключить из рассмотрения (убрать) целиком закрытые ковры.

Предположив, что «верхнего» ковра нет, т. е. что на каждом ковре есть и открытый, и закрытый участки, мы тут же придём к противоречию: к левому концу коридора примыкает ковёр, у которого открытый участок — левый; примыкая к этому участку на этом ковре, лежит другой «открытый слева» ковёр, и так далее. Эта цепочка не может оборваться (между тем к правому концу коридора примыкает, конечно, ковёр, «открытый справа»).

Лемма о коврах доказана. Ясно, что многоугольник, соответствующий «верхнему» ковру, можно без помех двигать вверх в направлении $d$‍.‍

По поводу этой задачи сделаем несколько замечаний.

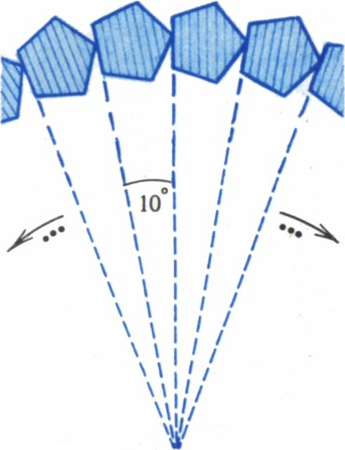
1. Аналог «леммы о коврах» для фигур на плоскости, очевидно, неверен. Неверен и аналог утверждения для выпуклых многогранников: Г. А. Гальперин указал пример нескольких «плит», ни одну из которых нельзя вытащить, не сдвигая остальных (в этом примере «наружные» грани 12 плит образуют додекаэдр, а «швы» — грани, которыми они «почти соприкасаются»,— выбраны так, что у каждой плиты по крайней мере два несоседних «шва» образуют с наружной гранью угол больше $90^\circ$‍).‍

2. В первоначальной формулировке авторов задачи В. Г. Ильичёва и Д. А. Терёшина была ещё дополнительная оговорка: $n$‍‍-угольник разрешено двигать лишь в направлении, перпендикулярном его стороне; при этом меняется и ответ: например, нетрудно придумать семейство 5-угольников, ни один из которых нельзя сдвинуть таким образом (рис. 2).