Задача М1124‍‍

Пусть прямая $l$‍‍ пересекает боковые стороны $AB$‍‍ и $CD$‍‍ трапеции в точках $K$‍‍ и $N$‍,‍ диагонали $AC$‍‍ и $BD$‍‍ — в точках $L$‍‍ и $M$‍,‍ продолжения оснований $AD=a$‍‍ и $BC=b$‍‍ — в точках $P$‍‍ и $Q$‍;‍ $PA=x$‍,‍ $CQ=y$‍‍ (см. рисунок). Тогда, рассматривая пары подобных треугольников, основания которых лежат на прямых $AD$‍‍ и $BC$‍,‍ а общей вершиной служит одна из точек $K$‍,‍ $L$‍,‍ $M$‍‍ или $N$‍,‍ получим: $$ \dfrac{PK}{KQ}=\dfrac x{b+y},\quad \dfrac{PN}{NQ}=\dfrac{x+a}y,\quad \dfrac{PL}{LQ}=\dfrac xy,\quad \dfrac{PM}{MQ}=\dfrac{x+a}{y+b}.\tag{*} $$

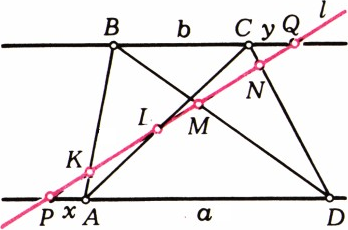
а) Если произведение первых двух отношений (*) равно 1, то $$\dfrac{PL}{LQ}\cdot\dfrac{PM}{MQ}=\dfrac{x(x+a)}{y(y+b)}=1,\quad\dfrac{PL}{LQ}=\dfrac{MQ}{PM},$$ откуда $$\dfrac{PL}{PQ}=\dfrac{MQ}{PQ},\quad PL=MQ,\quad KL=MN.$$

б) Четыре отношения (*) равны соответственно $\dfrac14$‍,‍ 4, $\dfrac23$‍‍ и $\dfrac32$‍‍ тогда (и только тогда), когда $$4x=b+y,\quad 4y=a+x,\quad 2y=3x,\quad 2(x+a)=3(y+b).$$ Если $x=2d$‍‍ и выполнены первые три из этих равенств, то $y=3d$‍,‍ $a=10d$‍,‍ $b=5d$‍.‍ При этом выполнено и четвёртое равенство.

Таким образом, нужная прямая существует в том и только в том случае, когда одно из оснований трапеции вдвое больше другого.