Задача М1113‍‍‍

Ответ: при 21. Поскольку число пар городов равно $\dfrac{21\cdot 20}{2}=210$‍,‍ каждая пара обслуживается хотя бы одной компанией, а каждая компания обслуживает ровно 10 маршрутов, число компаний не может быть меньше $210:10=21$‍.‍

Остаётся привести пример схемы обслуживания городов 21 авиакомпанией. Изобразим города вершинами правильного 21-угольника и занумеруем их по часовой стрелке (рис. 1). Пусть 1-я компания обслуживает города с номерами 1, 3, 8, 9, 12, 2-я — города с номерами 2, 4, 9, 10, 13, получающиеся из первого набора поворотом на угол $\dfrac{360^\circ}{21}$‍‍ (по часовой стрелке) и, вообще, $k$‍‍-я компания — города, которые получаются из первого набора поворотом на $(k-1)\cdot\dfrac{360^\circ}{21}$‍.‍ Любая пара вершин многоугольника попадает в один из этих наборов, так как среди расстояний между точками первого набора встречаются по разу длины всех сторон и диагоналей 21-угольника.

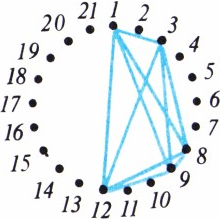
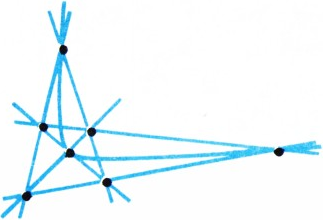
Легко проверить, что построенная нами схема удовлетворяет следующим условиям: 1) любые две точки входят хотя бы в один набор (это требуется в задаче), 2) любые два набора имеют одну и только одну общую точку. Если заменить здесь слово «набор» словом «прямая» и добавить ещё одно условие — 3) имеется 4 точки, никакие 3 из которых не лежат на одной прямой,— мы получим аксиомы так называемой (абстрактной) проективной плоскости: по определению, это произвольное множество точек, в котором выделены некоторые подмножества — «прямые», удовлетворяющие условиям 1)—3). В частности, наша схема — это конечная проективная плоскость из 21 точки. Нетрудно доказать, что любые две прямые конечной проективной плоскости состоят из одинакового числа точек, причём если это число равно $n$‍,‍ то число точек на плоскости равно $n^2-n+1$‍‍ и таково же число прямых. На рисунке 2 показана схема самой маленькой проективной плоскости — из семи точек.