Задача М1061‍‍

Будем устанавливать направления на дорогах постепенно. Пусть это уже сделано для дорог, соединяющих города из некоторого множества $M$‍‍ так, что требование задачи выполнено: из любого города этого множества можно проехать в любой другой из них, следуя по выбранным направлениям. (Для начала можно считать, что $M$‍‍ состоит из одного города, а направления нигде не установлены.) Докажем, что если ещё не все города входят в $M$‍,‍ то можно выбрать направления ещё на нескольких дорогах и увеличить М с соблюдением этого требования.

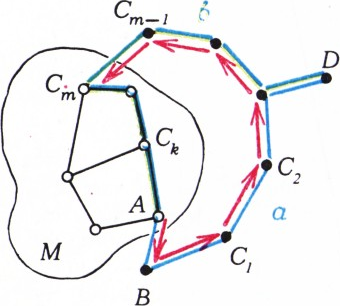
Ясно, что найдётся дорога, соединяющая город $A$‍‍ из $M$‍‍ с городом $B$‍,‍ не входящим в $M$‍.‍ Построим путь $c=BC_1C_2\ldots C_kA$‍‍ из $B$‍‍ в $A$‍,‍ не проходящий по дороге $AB$‍.‍ Для этого возьмём любой город $D$‍,‍ отличный от $A$‍‍ и $B$‍,‍ и рассмотрим путь $a$‍‍ из $A$‍‍ в $D$‍,‍ нe проходящий через $B$‍,‍ и путь $B$‍‍ из $D$‍‍ в $B$‍,‍ не проходящий через $A$‍‍ (рис. 1). В качестве $c$‍‍ можно взять путь, идущий сначала по $a$‍‍ — до первого города, общего для $a$‍‍ и $b$‍,‍ — а потом по $b$‍.‍ Пусть $C_m$‍‍ — первый из городов $C_1$‍,‍ $\ldots$‍,‍ $C_{k}$‍,‍ входящий в $M$‍‍ (если таких городов нет, положим $m=k+1$‍,‍ $C_m=A$‍).‍ Выберем направления на дорогах $AB$‍,‍ $BC_1$‍,‍ $C_1C_2$‍,‍ $\ldots$‍,‍ $C_{m-1}C_m$‍‍ по порядку: от $A$‍‍ к $B$‍,‍ от $B$‍‍ к $C_1$‍‍ и т. д., и присоединим к $M$‍‍ города $B$‍,‍ $C_1$‍,‍ $\ldots$‍,‍ $C_{m-1}$‍.‍ Наше условие на нарушится, так как из любого присоединённого города можно попасть в «старое» множество $M$‍‍ (дойдя до $C_m$‍)‍ и в любой из них можно попасть из $M$‍‍ (через $A$‍).‍

Повторяя этот процесс, мы включим в $M$‍‍ все города. На оставшихся после этого «неотрегулированных» дорогах (если такие ещё будут) направления движения установим произвольно.

Можно рассуждать несколько иначе, доказав сначала, что в условиях задачи любые два города соединены двумя путями, идущими по разным дорогам (это утверждение составляло содержание одной из задач Всесоюзной олимпиады).

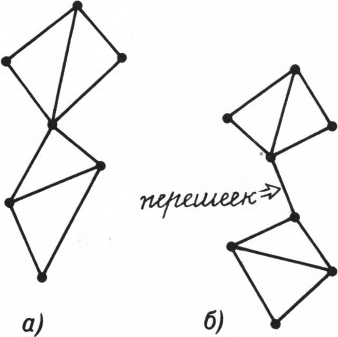
Наша задача даёт только достаточное условие. Оказывается, верна такая теорема: для того чтобы на дорогах можно было расставить стрелки так, чтобы, двигаясь в предписанных ими направлениях, можно было доехать из любого города в любой другой, необходимо и достаточно, чтобы исходная сеть дорог была связной и не имела перешейков (т. е. после закрытия любой дороги из каждого города можно было бы добраться до любого другого, рис. 2). Эту не очень сложную теорему доказал в 1939 г. Г. Роббинс‍), известный, в частности, как соавтор Р. Куранта по замечательной книге «Что такое математика».