Задача М983‍‍

а) Пусть 16 теннисистов стоят по кругу и каждый выиграл у 7 следующих за ним по часовой стрелке (как сыграли между собой теннисисты, отстоящие на 8 мест, несущественно). Такое распределение результатов удовлетворяет условию задачи: если произвольно отметить в круге 10 теннисистов — $A_1$‍,‍ $A_2$‍,‍ $\ldots$‍,‍ $A_{10}$‍‍ (по часовой стрелке), — то между $A_1$‍‍ и $A_2$‍,‍ $A_2$‍‍ и $A_3$‍,‍ $\ldots$‍,‍ $A_{10}$‍‍ и $A_1$‍‍ будет не более чем по 6 теннисистов, поэтому в каждой из этих пар первый выиграл у второго.

Число 16 в условии задачи можно заменить на любое $n\ge3$‍,‍ а 10 — на любое $k$‍‍ такое, что $\dfrac{n+3}2\le k\le n$‍,‍ — пример строится точно так же. Если $k\lt\dfrac{n+3}2$‍,‍ такого примера построить нельзя.

б) Докажем, что если любых $k$‍‍ ($2\lt k\lt n$‍)‍ из $n$‍‍ теннисистов, сыгравших друг с другом по одной партии, можно расставить в соответствии с условием, то любых $k+1$‍‍ — тоже.

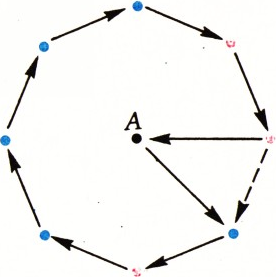
Рассмотрим некоторую группу из $k+1$‍‍ теннисистов и удалим из неё одного — $A$‍,‍ а остальных $k$‍‍ расставим по циклу (так, чтобы каждый выиграл у следующего). Отметим тех из $k$‍,‍ которым $A$‍‍ проиграл, красным, а тех, у кого он выиграл — синим (см. рисунок); хотя бы один красный и хотя бы один синий заведомо найдутся, потому что $A$‍‍ вместе с любыми $k-1$‍‍ теннисистами можно расставить по циклу (т. е. даже среди любых $k-1$‍‍ из наших $k$‍‍ найдётся и красный, и синий теннисист). Теперь выберем в нашем цикле любое место, где за красным по часовой стрелке стоит синий, и вставим между ними $A$‍.‍

Заметим, что при $n=16$‍,‍ $k=10$‍‍ утверждение задачи останется верным, даже если не требовать, чтобы все теннисисты сыграли друг с другом. Чтобы убедиться в этом, достаточно из условия, что любых 10 теннисистов можно расположить по циклу, вывести такие следствия:

1. каждый выиграл не более 7 и проиграл не менее 7 партий;
2. среди любых 11 найдётся такой, который сыграл со всеми 10 остальными.