Задача М970‍‍‍

а) Ответ. 2. Две последние остановки сохраняются при любом порядке голосования: против последней никто не голосует, против предпоследней голосует один пассажир, а за неё — не меньше одного. Если водитель называет остановки в следующем порядке номеров: 31, 32, 29, 30, 27, 28, $\ldots$‍,‍ 1, 2, все остальные остановки отменят (см. таблицу).

б) Ответ. 6. Пусть после голосования осталось неотменёнными $m$‍‍ остановок, и на $i$‍‍-й из них, считая с конца, сошло $a_i$‍‍ пассажиров (например, $a_1=1$‍‍ — на последней, 32-й остановке, очевидно, сходит 1 пассажир). Тогда против отмены этой остановки проголосовало не больше $a_i$‍‍ пассажиров (ибо последующее голосование не могло уже изменить решения сойти на ней), а за отмену — не меньше $a_{i-1}+a_{i-2}+\ldots+a_1$‍.‍ Поскольку остановку не отменили, $a_i\ge a_{i-1}+a_{i-2}+\ldots+a_1$‍.‍ Пусть осталось $m$‍‍ остановок, тогда $$ \begin{gather*} 32=a_m+a_{m-1}+a_{m-2}+\ldots+a_1\ge2(a_{m-1}+a_{m-2}+\ldots+a_1)\ge\\ \ge2^2(a_{m-2}+\ldots+a_1)\ge\ldots\ge2^{m-1}a_1=2^{m-1}, \end{gather*} $$ и следовательно, $m\le6$‍.‍

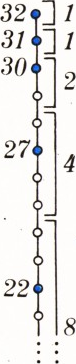
Укажем такой порядок голосования, при котором $m=6$‍.‍ Разобьём остановки, начиная с последней, на 6 групп, состоящих из 1, 1, 2, 4, 8, 16 остановок. В каждой группе отметим одну остановку так, чтобы соседние отмеченные остановки были равноудалены от общей границы их групп, т. е. остановки с номерами 32, 31, 30, 27, 22, 11 (см. рисунок). Проведём голосование от конца к началу сперва по неотмеченным остановкам (легко видеть, что их все отменяют), потом — по отмеченным (за каждую из них проголосуют все паcсажиры её группы, против — все пассажиры следующих групп; поскольку $2^k=1+1+2+\ldots+2^{k-1}$‍,‍ число голосов за и против будет одинаковым и остановку не отменят).

Проведённые рассуждения справедливы для любого числа остановок; ответ в задаче б) в общем случае — $[\log_2n]+1$‍.‍