Задача М937‍‍

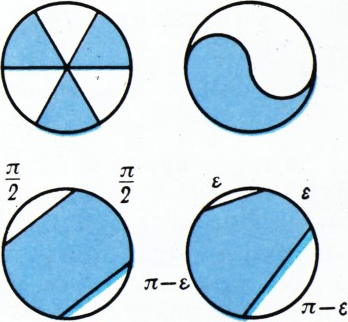
Ответ на оба вопроса а) и б) положительный. Примеры представлены на рисунке. Для ответа на вопрос а), кроме разнообразных вариантов фигуры в виде «пропеллера» или древнекитайского символа «Янь и инь», годится и такой вырожденный пример: из круга радиуса 1 с центром $O$‍‍ выкалываются три точки — вершины равностороннего треугольника с центром $O$‍.‍

Для ответа на вопрос б) подходит такая фигура: окружность радиуса 1 с центром $O$‍‍ разбивается на четыре дуги величиной $\eps$‍,‍ $\eps$‍,‍ $\pi-\eps$‍,‍ $\pi-\eps$‍‍ и строится «выпуклая оболочка» двух несмежных дуг. (Левый нижний рисунок соответствует $\eps=\pi/2$‍.)‍ Заметим, что при малом $\eps$‍‍ построенная фигура имеет площадь, сколь угодно близкую к площади полукруга.

Доказательство, что построенная фигура не покрывает полукруг, во всех случаях опирается на такое соображение: концы диаметра полукруга находятся на расстоянии 2, следовательно, их могут закрыть лишь такие две точки построенной фигуры, которые являются диаметрально противоположными точками круга радиуса 1, из которого мы её вырезаем; таким образом, наша фигура должна была бы содержать целый полукруг с центром $O$‍‍ радиуса 1.

Тот факт, что двумя экземплярами фигуры можно покрыть круг, очевиден (во всех примерах достаточно повернуть фигуру относительно центра круга на некоторый угол или отразить от некоторой прямой, проходящей через центр).