Задача М926‍‍

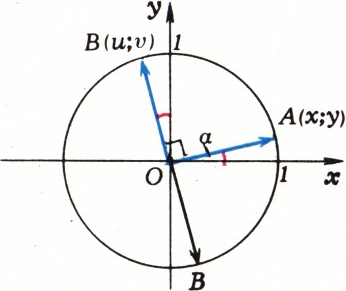
Условие задачи удобно представить геометрически. Отметим на координатной плоскости $Oxy$‍‍ точки $A(x;y)$‍‍ и $B(u;v)$‍.‍ Угол $AOB$‍‍ прямой, так как $\overrightarrow{OA}\cdot\overrightarrow{OB}=xu+yv=0$‍.‍ Кроме того, $OA^2=x^2+y^2=1$‍‍ и $OB^2=1$‍,‍ поэтому точка $B$‍‍ получается из точки $A$‍‍ поворотом вокруг $O$‍‍ на $\pm90^\circ$‍‍ (см. рисунок) и $x=\cos\alpha$‍,‍ $y=\sin\alpha$‍,‍ где $\alpha$‍‍ — угол между вектором $\overrightarrow{OA}$‍‍ и осью $Ox$‍,‍ а значит, $u=\cos(\alpha\pm90^\circ)=\mp\sin\alpha=\mp y$‍,‍ $v=\sin(\alpha\pm90^\circ)=\pm\cos\alpha=\pm x$‍.‍ Следовательно, $$ \begin{gather*} x^2+u^2=x^2+y^2=1,\\y^2+v^2=y^2+x^2=1,\\xy+uv=xy-xy=0. \end{gather*} $$

Приведём ещё одно, чисто алгебраическое, решение. В тождестве $$ \begin{gather*} (x^2+y^2-1)^2+(u^2+v^2-1)^2+2(xu+yv)^2=\\ =x^4+y^4+u^4+v^4+2-2(x^2+y^2+u^2+v^2)+2(x^2y^2+u^2v^2+x^2u^2+y^2v^2)+4xuyv=\\ =(x^2+u^2-1)^2+(y^2+v^2-1)^2+2(xy+uv)^2 \end{gather*} $$ левая часть, по условию, равна нулю; следовательно, равна нулю и правая часть, т. е. справедливы три доказываемых равенства.

Попробуйте обобщить нашу задачу на трёхмерный случай — доказать, что если три вектора длины 1 в пространстве с координатами $(x_1;x_2;x_3)$‍,‍ $(y_1;y_2;y_3)$‍,‍ $(z_1;z_2;z_3)$‍‍ попарно перпендикулярны, то векторы $(x_1;y_1;z_1)$‍,‍ $(x_2;y_2;z_2)$‍‍ и $(x_3;y_3;z_3)$‍‍ тоже имеют длину 1 и попарно перпендикулярны.