Задача М907‍‍

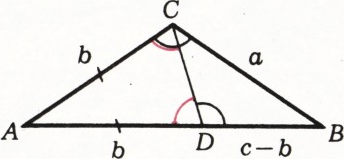
Доказываемое соотношение удобно переписать в виде равенства отношений отрезков $$ \dfrac ac=\dfrac{c-b}{a}.\tag{*} $$ Теперь его можно доказывать с помощью подобных треугольников. Возьмём на стороне $AB$‍‍ такую точку $D$‍,‍ что $AD=b$‍‍ (а $DB=c-b$‍;‍ см. рисунок). Равенство (*) — это условие пропорциональности сторон треугольников $ABC$‍‍ и $CBD$‍,‍ заключающих общий угол $B$‍‍ этих треугольников, поэтому достаточно доказать, что эти треугольники подобны, т. е. что, например, углы $ACB$‍‍ и $CDB$‍‍ равны. Имеем $$ \begin{gather*} \angle CDB=180^\circ-\angle ADC=180^\circ-\dfrac{180^\circ-\angle A}{2}=\\ =180^\circ-(\angle A+\angle B)=\angle ACB. \end{gather*} $$ (Мы воспользовались тем, что треугольник $ACD$‍‍ равнобедренный и данным соотношением $3\angle A+2\angle B=180^\circ$‍.)‍