Условие задачи (1984, № 10) Задача М887 // Квант. — 1984. — № 10. — Стр. 40—41; 1985. — № 2. — Стр. 41.
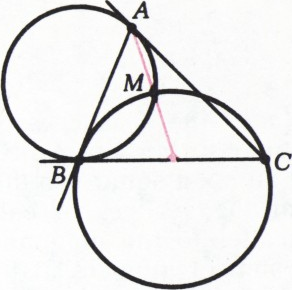
Две касательные к окружности,
Изображения страниц
Решение задачи (1985, № 2) Задача М887 // Квант. — 1984. — № 10. — Стр. 40—41; 1985. — № 2. — Стр. 41.
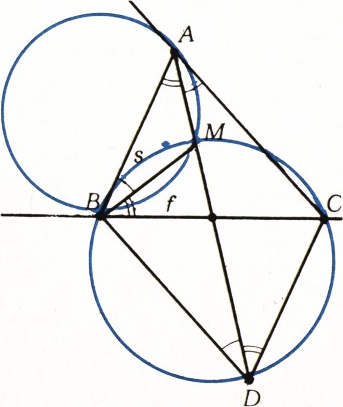
Пусть прямая
Пользуясь тем, что величина угла с вершиной на окружности, образованного двумя хордами или хордой и касательной, равна половине величины дуги, заключенной внутри угла, можно записать две цепочки равенств:
$$\begin{gather*}
\angle ADB=\dfrac12{\smile}{BsM}=\angle ABM=\dfrac12{\smile}{AM}=\angle CAD,\\
\angle ADC=\dfrac12{\smile}{MC}=\angle MBC=\dfrac12{\smile}{BfM}=\angle BAM
\end{gather*}
$$


