Условие задачи (1984, № 7) Задача М871 // Квант. — 1984. — № 7. — Стр. 50; 1984. — № 10. — Стр. 43—44.
Текстовое представление условия задачи находится в процессе подготовки. С графическим представлением можно ознакомиться в опубликованном номере
Изображения страниц
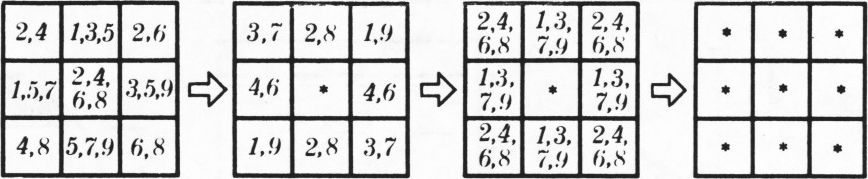
Решение задачи (1984, № 10) Задача М871 // Квант. — 1984. — № 7. — Стр. 50; 1984. — № 10. — Стр. 43—44.
Текстовое представление решения задачи находится в процессе подготовки. С графическим представлением можно ознакомиться в опубликованном номере