Задача М839‍‍‍

Ответ: да, можно.

Для краткости договоримся называть подмножество натурального ряда «хорошим», если оно не содержит ни одной тройки последовательных членов арифметической прогрессии (иными словами, если ни одно число этого подмножества не является средним арифметическим двух других). Докажем, что

из множества 1, 2, $\ldots$‍,‍ $5\cdot3^k$‍‍ ($k\ge0$‍)‍ можно выбрать «хорошее» подмножество $X_k$‍,‍ состоящее из $4\cdot2^k$‍‍ чисел.

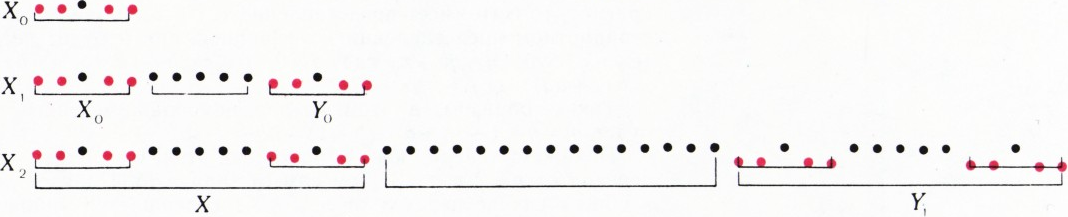
На рисунке показаны первые шаги индуктивного построения нужного множества: $X_0=\{1,2,4,5\}$‍,‍ а $X_{k+1}=X_k\cup Y_k$‍,‍ где множество $Y_k$‍‍ получается из $X_k$‍‍ сдвигом на $2a_k$‍,‍ $a_k$‍‍ — наибольшее число в $X_k$‍.‍ Таким образом, $a_{k+1}=3a_k$‍‍ и $a_k=5\cdot3^k$‍,‍ т. е. $X_k\subset\{1,2,\ldots,5\cdot3^k\}$‍;‍ кроме того, на каждом шаге количество чисел в нашем «хорошем» множестве удваивается, т. е. $X_k$‍‍ состоит из $4\cdot2^k$‍‍ чисел. Докажем по индукции, что все множества $X_k$‍‍ «хорошие». Для $X_0$‍‍ это очевидно. Проверим, что среднее арифметическое двух чисел из $X_{k+1}$‍‍ не входит в $X_{k+1}$‍.‍ Поскольку по предположению индукции множество $X_k$‍,‍ а с ним и $Y_k$‍,‍ — «хорошее», можно считать, что одно из этих чисел, $x$‍,‍ содержится в $X_k$‍,‍ а другое, $y$‍,‍ — в $Y_k$‍.‍ Тогда $0\lt x\le a_k$‍,‍ $2a_k\lt y\le3a_k$‍,‍ поэтому $a_k\lt\dfrac{x+y}2\le2a_k$‍,‍ но числа от $a_k+1$‍‍ до $2a_k$‍‍ по построению не входят в $X_{k+1}$‍.‍

Остаётся заметить, что множество $X_9$‍‍ содержит $4\cdot2^9=2048\gt1983$‍‍ чисел, и все они не превосходят $a_9=5\cdot3^9=98415\lt10^5$‍.‍

В связи с задачей М839 (Квант, 1983, № 12, с. 35) десятиклассник (теперь уже студент) Л. Вертгейм из Новосибирска прислал нам ряд интересных результатов о последовательности $a$‍,‍ определяемой условиями: $a_1=1$‍,‍ $a_2=2$‍,‍ $a_k$‍‍ — наименьшее из натуральных чисел, не образующих тройку членов арифметической прогрессии с предыдущими и большее $a_{k-1}$‍‍ (при $k\gt2$‍):‍ 1, 2, 4, 5, 10, 11, 13, 14, 28, 29, $\ldots$‍‍ В частности: $a_{2^m+1}=2a_{2^m}=3^m+1$‍;‍ $a_{2k}=a_{2k-1}+1$‍;‍ если $n$‍‍ нечётно, то чтобы найти $a_n$‍,‍ достаточно записать $n$‍‍ в двоичной системе, а прочитать — в троичной (например, $11_{10}=1011_2$‍,‍ $a_{11}=1011_3=31$‍);‍ любое натуральное число можно получить как сумму двух (не обязательно различных) чисел $a_n$‍.‍

Правда, всё это не решает более трудный вопрос: каково наименьшее (для данного $n$‍)‍ число $b_n$‍‍ такое, что из отрезка натурального ряда от 1 до $b_n$‍‍ можно выбрать $n$‍‍ чисел, не содержащих тройки членов арифметической прогрессии, — получается лишь оценка сверху: $b_n\le a_n\le c\cdot n^{\log_23}$‍.‍

Новый результат в похожей на М839 задаче «о равновесах» (Квант, 1981, № 12, с. 34) сообщил нам В. Д. Яковлев из Сыктывкара: ему удалось построить пример, улучшающий известный (считавшийся кандидатом в «абсолютные чемпионы»), приведённый в «Кванте». Вот этот пример: последовательность $\beta_n$‍‍ задаётся для $n\ge0$‍‍ так: 0, 2, 3, 4, 8, 14, 25, 47, 86, 164, 314, 603, 1159; тогда числа $\beta_{12}-\beta_n$‍,‍ $n=0$‍,‍ 1, $\ldots$‍,‍ 11, образуют «систему равновесов» — любые две подсуммы этих 12 чисел различны. Так что и в этой задаче окончательного результата пока нет.