Условие задачи (1983, № 11) Задача М834 // Квант. — 1983. — № 11. — Стр. 36—37; 1984. — № 2. — Стр. 46—47.
Оросительная установка, расположенная в точке
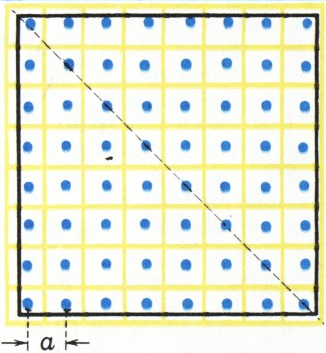
- Бригадир предложил расположить 64 установки в вершинах квадратной сетки со сторонами, параллельными краям поля (рис. 1). В каких пределах может меняться сторона
$a$ квадратной сетки? - Восьмиклассник Витя утверждает, что можно оросить поле с помощью лишь 46 таких установок. Прав ли Витя?

Изображения страниц
Решение задачи (1984, № 2) Задача М834 // Квант. — 1983. — № 11. — Стр. 36—37; 1984. — № 2. — Стр. 46—47.
а) Ответ: длина стороны
Углы поля должны отстоять не более чем на 100 м от ближайших к ним установок. Расстояние между противоположными углами поля равно
Центр каждого квадрата сетки должен отстоять от его вершин также не более чем на 100 м, поэтому должно выполняться условие
Если оба условия на
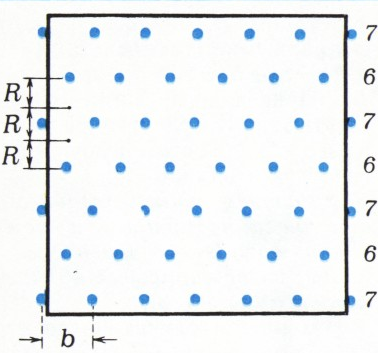
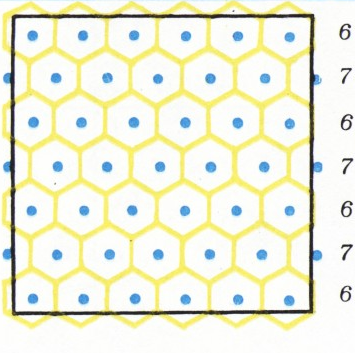
б) Витя предложил расставлять установки не по квадратной, а по треугольной сетке; на рисунке 2 показано, как разместить ровно
В горизонтальном направлении ряд из 6 установок обслуживает расстояние
С различными проявлениями «оптимальности» шестиугольной решётки в математических задачах и физических явлениях можно познакомиться, например, в книге Г. Штейнгауза «Математический калейдоскоп» из серии Библиотечка «Квант» (М., 1981). Напишите нам, встречались ли вам интересные её использования в живой природе (не считая, конечно, всем известных пчелиных сот), в технике.



