Задача М828‍‍‍

Ответ: а), б) можно. В обоих случаях искомую расстановку можно получить, комбинируя две более простые расстановки.

а) Поставим единицы на параллельных диагоналях сетки, удалённых друг от друга на 4 клетки (по горизонтали или вертикали), а в остальные клетки поставим нули (рис. 1, а). Тогда сумма чисел в каждом прямоугольнике $4\times6$‍‍ будет равна 6. Это первая расстановка. Вторая устроена так же, но в ней расстояние между диагоналями с единицами - 6 клеток (рис. 1, б); для неё сумма чисел в любом прямоугольнике $4\times6$‍‍ равна 4. Теперь наложим одну расстановку на другую и сложим числа, попавшие в одну клетку; очевидно, для итоговой расстановки рассматриваемая сумма чисел вегда равна 10.

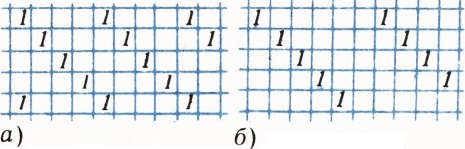
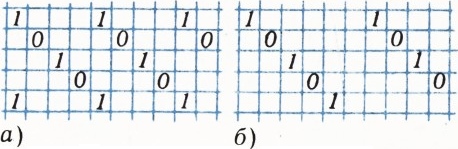
б) Возьмём те же расстановки, что и в пункте а), но на диагоналях вместо сплошных единиц поставим поочерёдно единицы и нули (рис. 2). Сумма чисел в любом прямоугольнике $4\times6$‍‍ будет теперь в одном случае равна 3 (рис. 2, а), а в другом — 2 (рис. 2, б). Накладывая одну расстановку на другую и вычитая из каждого числа первой расстановки попавшее в ту же клетку число второй, получим требуемую расстановку.

Предлагаем читателям, используя те же идеи, доказать такое общее утверждение: в клетках бесконечной плоской решётки можно так расставить целые числа, что сумма чисел в любом прямоугольнике данных размеров принимает одно и то же заданное значение. То же верно для пространственной решётки из параллелепипедов. Подумайте, останется ли верным это утверждение, если ограничиться только неотрицательными числами.