Задача М820‍‍‍

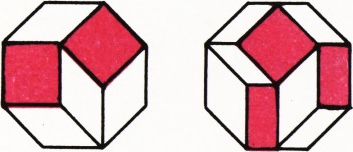
а) Примеры простейших разрезаний правильного восьмиугольника на параллелограммы показаны на рисунке 1. Для доказательства утверждения представим правильный восьмиугольник пересечением двух квадратов $P$‍‍ и $Q$‍.‍ Пусть для определённости у квадрата $P$‍‍ две стороны вертикальные, две горизонтальные (рис. 2). Будем строить из параллелограммов разбиения «дорожку», начинающуюся от левой стороны квадрата $P$‍,‍ так, чтобы каждый параллелограмм примыкал к предыдущему по вертикальной стороне или её части. Ясно, что последний параллелограмм этой дорожки будет примыкать к правой стороне квадрата $P$‍.‍ Такого же рода дорожка соединит нижнюю сторону квадрата $P$‍‍ с верхней.(Мы будем называть такие две дорожки перпендикулярными.) Общий параллелограмм этих двух дорожек является прямоугольником, так как его стороны параллельны сторонам квадрата $P$‍.‍ Второй прямоугольник получим, повторив это построение для квадрата $Q$‍.‍

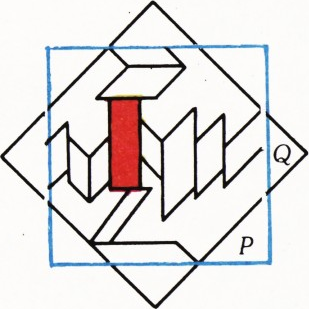
б) Правильный $4k$‍‍-угольник является пересечением $k$‍‍ одинаковых квадратов, каждый из которых даёт свою пару перпендикулярных дорожек, а каждая пара дорожек даёт прямоугольник (см. пункт а)). Итого, мы нашли $k$‍‍ прямоугольников.

в) Ответ. сумма площадей всех прямоугольников разбиения равна $k$‍.‍

Сначала разрежем параллелограммы разбиения на более мелкие параллелограммы так, чтобы новое измельчённое разбиение удовлетворяло следующему требованию: любые два его параллелограмма либо не имеют общих точек, либо имеют общую вершину, либо имеют общую сторону целиком. При этом стороны каждого параллелограмма нового разбиения параллельны сторонам содержащего его параллелограмма старого разбиения. Поэтому объединение всех новых прямоугольников совпадает с объединением всех старых прямоугольников, а значит, достаточно решить задачу для нового разбиения.

Рассмотрим любую дорожку $\textit{д}$‍‍ (рис. 3). Каждые два её соседних параллелограмма имеют целую общую сторону, длину которой назовём шириной дорожки. Таким образом, длина одной из сторон каждого прямоугольника, входящего в дорожку $\textit{д}$‍,‍ равна её ширине, а сумма длин их вторых сторон равна суммарной ширине всех дорожек, перпендикулярных $\textit{д}$‍,‍ т. е. единице - длине стороны $4k$‍‍-угольника. Следовательно, общая площадь всех прямоугольников дорожки численно равна её ширине.

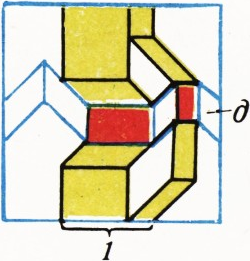
Возьмём теперь один из $k$‍‍ квадратов, дающих в пересечении наш $4k$‍‍-угольник. Сумма площадей всех прямоугольников, принадлежащих дорожкам, соединяющим две противоположные стороны квадрата, равна сумме ширин этих дорожек, т. е. 1. А поскольку каждый из прямоугольников разбиения получается как пересечение двух перпендикулярных дорожек (в соответствующем квадрате), сумма площадей всех прямоугольников равна числу квадратов $k$‍.‍

Докажите самостоятельно, что если правильный $4k$‍‍-угольник разрезан на минимально возможное число параллелограммов (в этом случае все они будут ромбами), то среди них найдутся ровно $k$‍‍ одинаковых квадратов.