Условие задачи (1982, № 4) Задача М740 // Квант. — 1982. — № 4. — Стр. 25—26; 1982. — № 10. — Стр. 30—31.
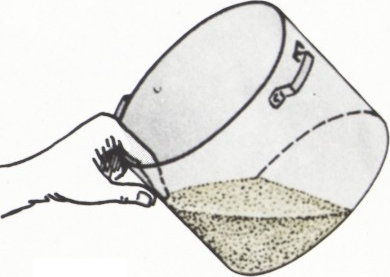
Серёжа насыпал в цилиндрическую кастрюлю немного пшена и спросил соседку тётю Люду: «Сколько нужно налить воды, чтобы получилась вкусная каша?» — «Это очень просто, — отвечала соседка. — Наклони кастрюлю — вот так; постучи, чтобы крупа пересыпалась и закрыла ровно половину дна. Теперь заметь точку на стенке кастрюли, ближайшую к краю, до которой поднялась крупа — и зажми её пальцем! До этого уровня и надо налить воду» (рис. 1). — «Так ведь пшена можно насыпать побольше и поменьше, да и кастрюли бывают разные — широкие и узкие», — усомнился Серёжа. — «Всё равно, мой способ годится в любом случае!» — гордо ответила тётя Люда.
- Докажите, что тётя Люда права: отношение объёмов воды и пшена по её рецепту всегда получится одинаковым.
- Чему равно это отношение?
Изображения страниц
Решение задачи (1982, № 10) Задача М740 // Квант. — 1982. — № 4. — Стр. 25—26; 1982. — № 10. — Стр. 30—31.
а), б) Будем считать, что пшено заполняет какую-то часть цилиндрической кастрюли без пустот, наподобие жидкости.
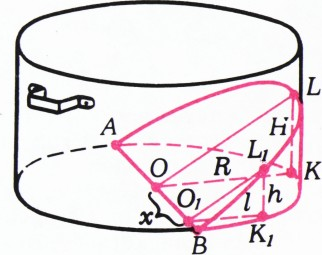
Пусть радиус кастрюли равен
Другое решение пункта а) легко получить из следующей общей теоремы: при растяжениях (сжатиях) вдоль оси объёмы всех тел умножаются на один и тот же коэффициент, равный коэффициенту растяжения (сжатия). Попробуйте доказать эту теорему.



