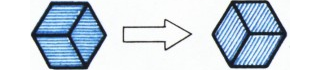
Автор задачи А. Смирнов предложил замечательную пространственную интерпретацию, которая делает решение задачи почти очевидным.
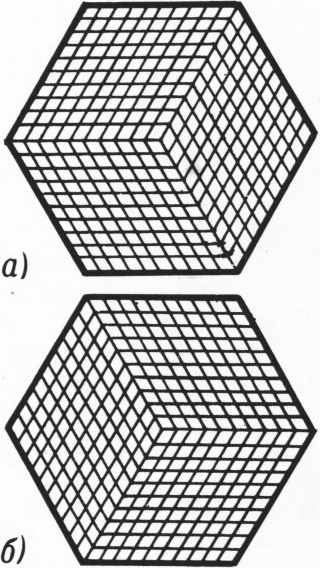
Представим себе куб размерами $k\times k\times k$, разбитый Ha $k^3$ кубиков $1\times1\times1$. Уложим его в «открытую коробку», склеенную из трёх квадратов $k\times k$ с общей вершиной $A$, и посмотрим на него по направлению диагонали $HA$ (рис. 4). Мы увидим рисунок 3. Если же высыпать из коробки все кубики (но считать, что на внутренних стенках коробки осталась сетка $k\times k$ — «следы» от кубиков), то мы увидим рисунок 2. Вообще, если снять сверху лишь часть из $k^3$ кубиков, то мы увидим как раз такую картину, о которой говорится в условии задачи (где $k=10$): шестиугольник, разбитый на $3k^2$ одинаковых ромбов (с острым углом $60^\circ$). При этом ромбам каждого из трёх типов — стороны которых параллельны определённым двум сторонам шестиугольника (на рисунках 5, 6 и 7 эти ромбы показаны белым, светло-голубым и тёмно-голубым цветом) — соответствуют грани кубиков, параллельные определённой паре граней большого куба; отсюда ясно, что соответствие между разбиениями шестиугольника на ромбы и соответствующими «частичными» заполнениями коробки взаимно однозначно. Операция, yказанная на рисунке 1, — это просто добавление кубика $1\times1\times1$ в свободное «гнездо» или вынимание такого кубика, на котором не лежат другие. (Например, на рисунке 7 происходит добавление кубика в «гнездо», обведённое красной линией.)
Теперь все утверждения задачи допускают вполне осязаемое обоснование (если не верите, сделайте модель!). Чтобы перейти от рисунка 2 к рисунку 3, нужно класть кубики в коробку по одному — и, разумеется, уложить их все можно самое меньшее за $k^3$ ходов (большее число ходов может получиться, если вынимать уже уложенные кубики). Если имеется два расположения ромбов: одному соответствует заполнение $C_1$, а другому — заполнение $C_2$ кубиками, то перейти от одного к другому можно любым из двух способов: либо сначала «спуститься» к рисунку 2 — вынуть все кубики, а затем уложить нужные $C_2$ кубиков, либо «подняться» до полного куба (рис. 3), а затем вынуть лишнее. Нетрудно проверить, что в случае $C_1+C_2\le k^3$ первый, а в случае $(k^3-C_1)+(k^3-C_2)\le k^3\iff C_1+C_2\ge k^3$ второй способ гарантирует переход от $C_1$ к $C_2$ не более чем за $k^3$ ходов. (Впрочем, наша модель позволяет указать для любых двух заполнений $C_1$ и $C_2$ точное «расстояние» $\rho(C_1,C_2)$ между ними — наименьшее число ходов, за которое можно перейти от одного к другому. Оно равно числу кубиков, на которое различаются $C_1$ и $C_2$, т. е. число кубиков $C_1$, которые лежат выше $C_2$, плюс число кубиков $C_2$, которые лежат выше $C_1$.)
Заметим, что «выход в пространство» для решения этой задачи не обязателен: многие читатели изложили (по существу, то же) решение, не выходя из плоскости, примерно так. Заметим, что ромбы, у которых имеется хоть одна «горизонтальная» сторона (голубые ромбы обоих оттенков на наших рисунках), образуют $k$ полосок, каждая из которых ведёт от верхней к нижней стороне шестиугольника и состоит из $2k$ ромбов. При этом рисунок 5 соответствует случаю, когда все полоски максимально смещены вправо, рисунок 6 — влево, а переход (рис. 7) позволяет на одной полоске в одном месте «изгиб вправо» заменить «изгибом влево» — сдвинуть на 1 ровно одну из пересекаемых полоской сторон ромбов. Теперь остаётся ввести какую-либо числовую оценку «смещения полосок» (аналогичную числу $C$ кубиков в пространственной модели), и решение задачи доводится до конца так же, как и выше.
Рисунки номер 1-7