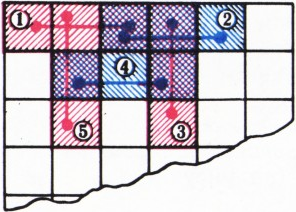
Условие задачи (1981, № 9) Задача М705 // Квант. — 1981. — № 9. — Стр. 20; 1982. — № 5. — Стр. 25—26.
На прямоугольном листе клетчатой бумаги расположено несколько прямоугольных карточек, стороны которых лежат на линиях сетки. Карточки покрывают лист в два слоя (т. е. каждую клетку листа покрывают в точности две карточки).
- Пусть каждая карточка имеет размеры
$1\times 2$ клетки. Докажите, что можно выбрать часть карточек так, чтобы они покрывали лист в один слой. (Передвигать карточки нельзя.)
Останется ли это верным, если карточки
- могут иметь произвольные размеры?
- имеют размеры
$1\times 3$ клетки?
Изображения страниц
Решение задачи (1982, № 5) Задача М705 // Квант. — 1981. — № 9. — Стр. 20; 1982. — № 5. — Стр. 25—26.
а) Мы докажем более общее утверждение: из покрытия любого конечного множества клеток карточками размером
Рассмотрим произвольную клетку. Пусть её покрывают карточки
Ясно, что это произойдёт в том случае, когда цепочка карточек замкнётся, т. е. когда очередная карточка окажется одной из уже выбранных. Ясно, что такой карточкой будет карточка
С оставшимися непокрытыми клетками множества поступаем аналогично до тех пор, пока все клетки исходного множества не будут покрыты карточками разного цвета. Утверждение а) доказано.
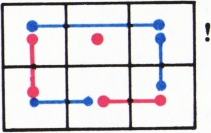
б) Ответ: нет. Соответствующий пример изображён на рисунке 1: прямоугольный лист размером
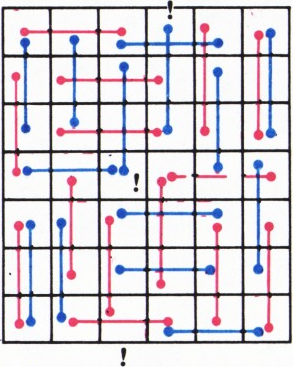
в) Ответ: нет. Пример для прямоугольника