Условие задачи (1981, № 9) Задача М704 // Квант. — 1981. — № 9. — Стр. 20—21; 1982. — № 5. — Стр. 24—25.
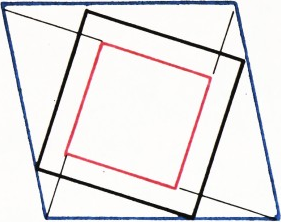
Вокруг квадрата описан параллелограмм (вершины квадрата лежат на разных сторонах параллелограмма). Докажите, что перпендикуляры, опущенные из вершин параллелограмма на стороны квадрата, образуют новый квадрат (рис. 1).
Изображения страниц
Решение задачи (1982, № 5) Задача М704 // Квант. — 1981. — № 9. — Стр. 20—21; 1982. — № 5. — Стр. 24—25.
Пусть вокруг чёрного квадрата (см. рис. 1) описан голубой параллелограмм
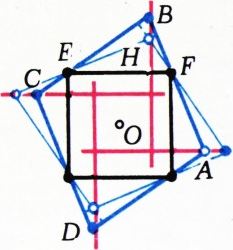
Пусть
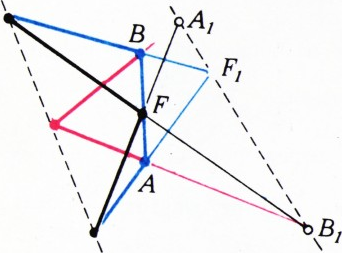
Теорема о том, что три высоты треугольника пересекаются в одной точке (мы надеемся, известная нашим читателям), не доказывается в школьном учебнике. Поэтому мы приведём ещё одно решение задачи, хотя и не столь изящное, но тоже простое.
Это решение годится и для более общего случая, когда роль квадрата играет чёрный параллелограмм (рис. 2): мы докажем, что красные прямые (соответственно параллельные сторонам чёрного параллелограмма) образуют параллелограмм, гомотетичный чёрному параллелограмму.
Для доказательства достаточно проверить, что красная точка
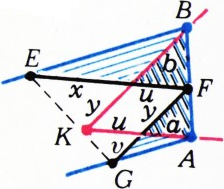
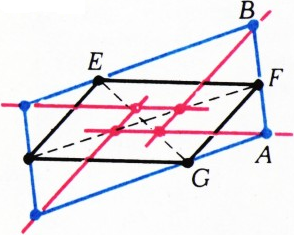
Полученный результат напоминает теорему Паппа, которую Д. Гильберт и С. Кон-Фоссен в своей замечательной (переизданной недавно по-русски) книге «Наглядная геометрия» формулируют так (с. 126—127): если вершины замкнутой шестизвенной ломаной лежат попеременно на двух прямых и две пары её противоположных звеньев параллельны, то и третья пара звеньев параллельна (на рис. 3 — как раз такая ломаная
На этом возможности обобщений не исчерпаны. Если «сфотографировать» конфигурацию рисунка 3 (т. е. спроектировать её из некоторой точки