Условие задачи (1981, № 7) Задача М694 // Квант. — 1981. — № 7. — Стр. 19—20; 1982. — № 3. — Стр. 33.
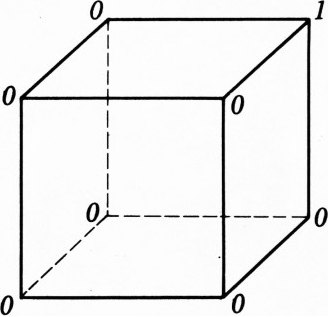
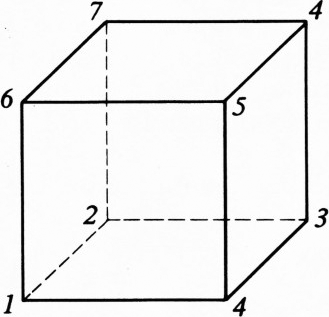
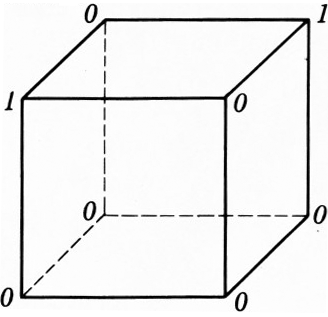
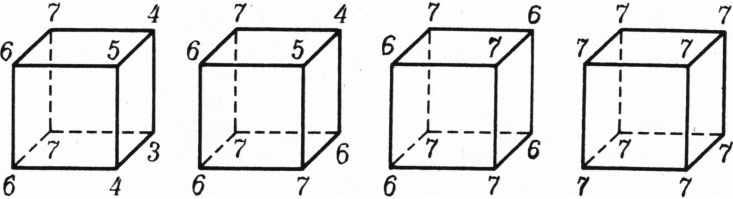
В каждой вершине куба записано число. За один шаг к двум числам, размещённым на одном (любом) ребре, прибавляется по единице. Можно ли за несколько таких шагов сделать все восемь чисел равными между собой, если вначале были поставлены числа, как на рисунке 1? Как на рисунке 2? Как на рисунке 3?
Изображения страниц
Решение задачи (1982, № 3) Задача М694 // Квант. — 1981. — № 7. — Стр. 19—20; 1982. — № 3. — Стр. 33.
Раскрасим вершины куба в синий и красный цвет таким образом, чтобы концы каждого ребра оказались окрашенными в разные цвета (рис. 4). При добавлении единицы к числам, размещённым на одном ребре, суммы чисел в синих и красных вершинах увеличиваются на 1, так что разность этих двух сумм не изменяется. Так как в кубах на рисунках 1 и 3 эта разность не равна нулю, от них нельзя прийти к кубу с равными числами в вершинах. Покажем теперь, что если в вершинах исходного куба записаны целые числа и суммы чисел в красных и синих вершинах равны, то все восемь чисел можно сделать равными между собой.
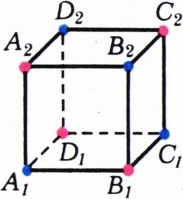
Обозначим через


