Задача М690‍‍‍

а) Заметим сначала, что для треугольников справедливо более сильное утверждение: $\dfrac{S_1}{P_1}\gt\dfrac{S_2}{P_2}$‍.‍ Это почти очевидно, так как $\dfrac{2S_1}{P_1}$‍‍ и $\dfrac{2S_2}{P_2}$‍‍ — радиусы кругов, вписанных в эти треугольники.

Для доказательства общего утверждения воспользуемся двумя фактами, которые мы докажем ниже:

1. во всякий выпуклый многоугольник площади $S$‍‍ и периметра $P$‍‍ можно поместить круг радиуса $R\gt\dfrac SP$‍;‍
2. для любого круга, содержащегося в данном многоугольнике, $R\le\dfrac{2S}P$‍.‍

Из 1) и 2) сразу следует утверждение а): поместим во внутренний многоугольник круг радиуса $R\gt\dfrac{S_2}{P_2}$‍;‍ поскольку $R\le\dfrac{2S_1}{P_1}$‍,‍ получаем требуемое.

Докажем 1). Построим на каждой стороне (выпуклого) многоугольника прямоугольник с высотой $h=\dfrac SP$‍‍ (рис. 1) ($S$‍‍ — площадь, $P$‍‍ — периметр многоугольника). Эти прямоугольники перекрываются; они могут даже «вылезать» за пределы многоугольника. Поскольку суммарная площадь прямоугольников равна $S$‍,‍ площадь покрытой ими части многоугольника меньше $S$‍.‍ Поэтому найдётся непокрытая точка, удалённая от всех сторон на расстояние $R\gt h$‍.‍

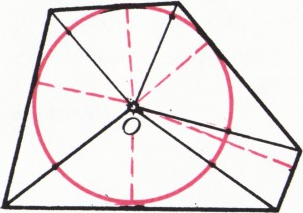
Докажем 2). Пусть $O$‍‍ — центр круга радиуса $R$‍,‍ содержащегося в многоугольнике (рис. 2). Поскольку длины высот треугольников с вершиной $O$‍,‍ основаниями которых служат стороны многоугольника, не меньше $R$‍,‍ получаем $S\gt\dfrac12PR$‍.‍ Поэтому $R\le\dfrac{2S}P$‍.‍ (Заметим, что если для какого-то круга, содержащегося в многоугольнике, $R=\dfrac{2S}P$‍,‍ то этот круг вписан в многоугольник — докажите это!).

В пространственном случае (см. б)) можно доказать, что если выпуклый многогранник объёма $V_1$‍‍ и площади поверхности $S_1$‍‍ содержит выпуклый многогранник объёма $V_2$‍‍ и площади поверхности $S_2$‍,‍ то $\dfrac{3V_1}{S_1}\gt\dfrac{V_2}{S_2}$‍.‍

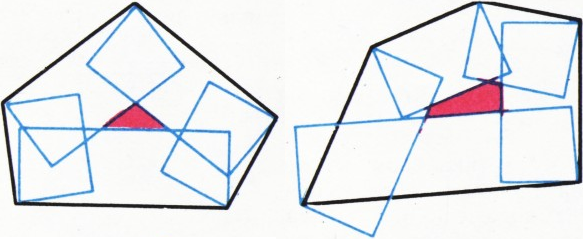
Доказательство получается заменой слов: периметр — площадь поверхности, площадь — объём, круг — шар, треугольник — пирамида, прямоугольник — призма. Заметим, что константы 2 (для плоского случая) и 3 (для пространственного) нельзя заменить меньшими. Примеры, подтверждающие это, показаны на рисунках 3 и 4 (узкий прямоугольник внутри узкого длинного треугольника и узкая призма внутри узкой высокой пирамиды).