Задача М689‍‍‍

Предположим, что прямоугольник удалось составить из $n$‍‍ трапеций. Отметим точки, в которые попадают вершины трапеций, в том числе — четыре вершины прямоугольника.

У каждой трапеции два острых угла (по $45^\circ$‍)‍ и два тупых (по $135^\circ$‍);‍ так что у всех $n$‍‍ трапеций вместе одинаковое число острых и тупых углов — по $2n$‍.‍

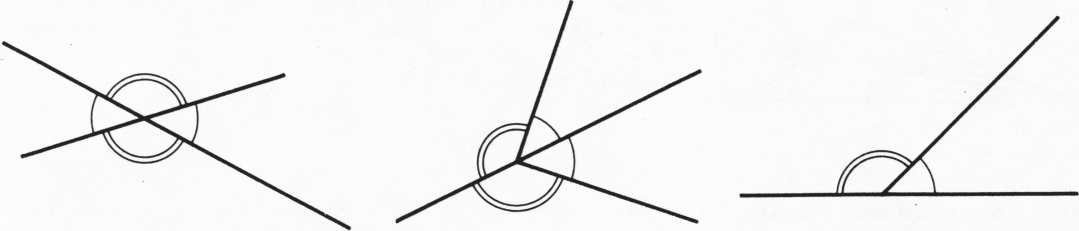
С другой стороны, ясно, что в каждой из отмеченных точек расположено не меньше острых углов, чем тупых (если там есть один тупой угол, то есть по крайней мере один острый, а если два тупых, то и два острых — см. рисунок); при этом в вершинах прямоугольника могут оказаться только острые углы трапеций. Таким образом, острых углов больше, чем тупых (по крайней мере, на 8).

Полученное противоречие доказывает невозможность составления прямоугольника из трапеций.