Условие задачи (1981, № 4) Задача М679 // Квант. — 1981. — № 4. — Стр. 22—23; 1981. — № 12. — Стр. 28—29.
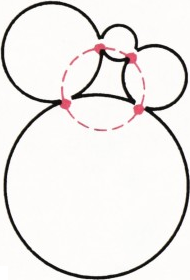
- На плоскости расположены четыре круга так, что первый касается второго в точке
$A$, второй — третьего в точке$B$, третий — четвёртого в точке$C$ и четвёртый — первого в точке$D$ (рис. 2). Докажите, что через четыре названные точки можно провести окружность или прямую. - В пространстве расположены четыре шара так, что первый касается второго в точке
$A$, второй — третьего в точке$B$, третий — четвёртого в точке$C$ и четвёртый — первого в точке$D$. Докажите, что через четыре названные точки можно провести окружность или прямую. - В пространстве расположены четыре шара так, что каждый касается трёх других. Докажите, что шесть точек касания принадлежат одной сфере или одной плоскости.
Изображения страниц
Решение задачи (1981, № 12) Задача М679 // Квант. — 1981. — № 4. — Стр. 22—23; 1981. — № 12. — Стр. 28—29.
а) Прежде всего ясно, что если какие-то три из точек
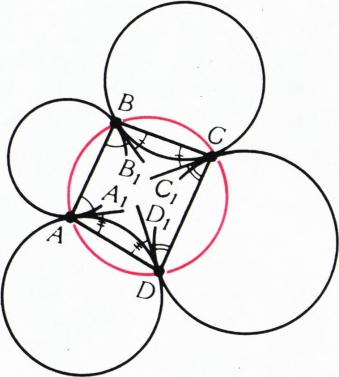
Пусть все четыре круга касаются внешним образом (рис. 2) и пусть
Из
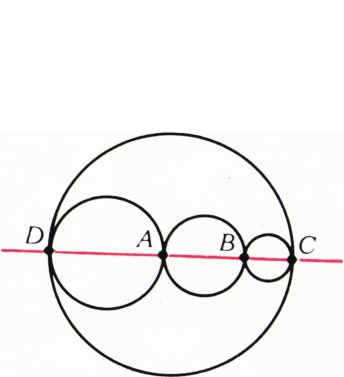
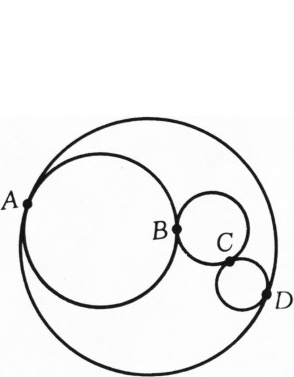
В случае, когда не все четыре круга касаются внешним образом (рис. 3), рассуждения аналогичны.
б) Если центры шаров лежат в одной плоскости, то и все точки касания лежат в этой плоскости, так что в этом случае задача б) сводится к задаче а).
Если же центры
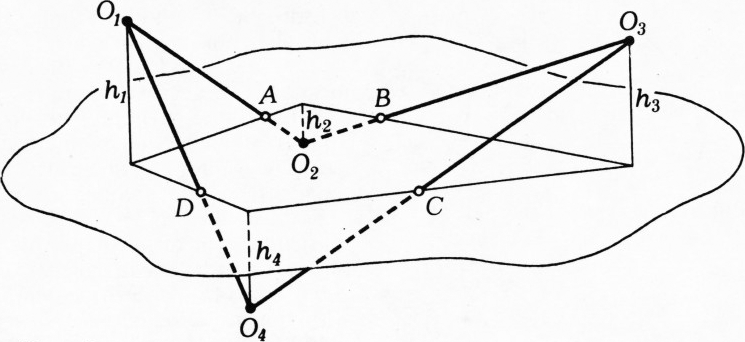
Пусть
Таким образом, плоскость
в) Пусть
По доказанному в пункте б) точки
У этих двух четвёрок точек есть две общие точки:
Если же эти четвёрки лежат на двух окружностях, находящихся.· в разных плоскостях и имеющих общую хорду



