Условие задачи (1981, № 3) Задача М671 // Квант. — 1981. — № 3. — Стр. 24; 1981. — № 11. — Стр. 23—24.
Во вписанном четырёхугольнике одна диагональ делит вторую пополам. Докажите, что квадрат длины первой диагонали равен половине суммы квадратов длин всех сторон четырёхугольника.
Изображения страниц
Решение задачи (1981, № 11) Задача М671 // Квант. — 1981. — № 3. — Стр. 24; 1981. — № 11. — Стр. 23—24.
Пусть
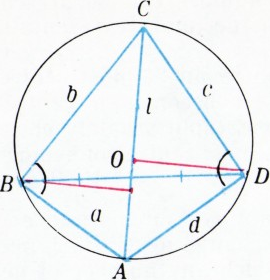
Легко заметить, что треугольники


