Задача М670‍‍‍

Представим себе, что данная система точек $X_1$‍,‍ $X_2$‍,‍ $\ldots$‍,‍ $X_n$‍‍ (рис. 1, а) «удвоилась»: каждая точка $X_i$‍‍ превратилась в две точки: $X_i'$‍‍ и $X_i''$‍‍ Расположим эти два комплекта точек так, как показано на рисунке 2, а: один под другим. При этом каждая линия, соединяющая пару соседей $X_i$‍‍ и $X_j$‍‍ в исходной системе, превращается в два наклонных отрезка, соединяющих точки $X_i'$‍‍ с $X_j''$‍‍ и $X_i''$‍‍ с $X_j'$‍.‍

Будем считать, что в чётные моменты времени перекрашиваются (по прежнему правилу) лишь точки верхнего ряда, в нечётные моменты времени — лишь точки нижнего ряда.

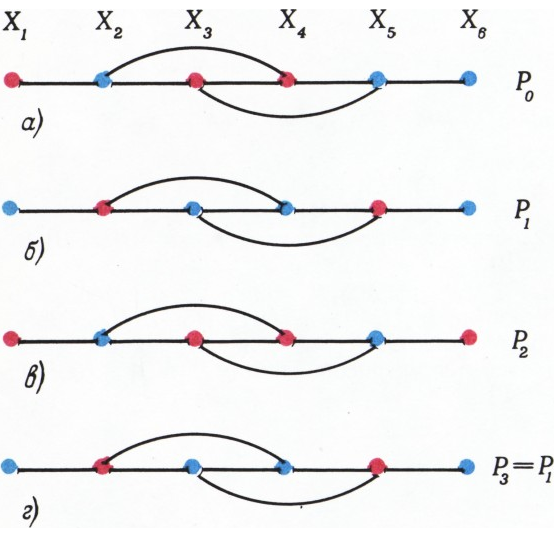
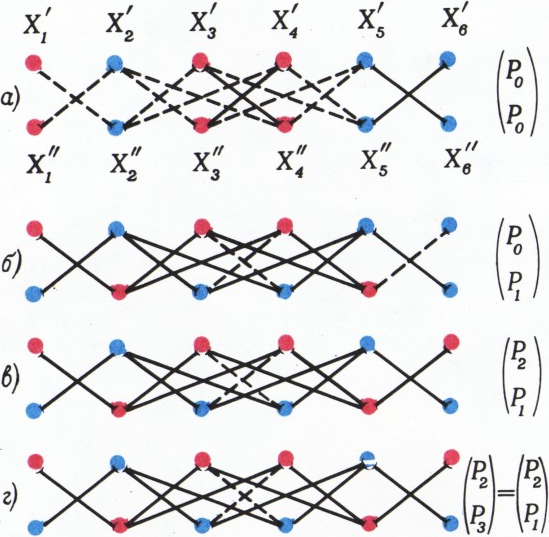
Легко видеть, что если на исходных точках возникает последовательность раскрасок $P_0$‍,‍ $P_1$‍,‍ $P_2$‍,‍ $P_3$‍,‍ $\ldots$‍‍ (рис. 1 , а‍—‍г), то на «удвоенной» системе возникает последовательность раскрасок $\dbinom{P_0}{P_0}$‍,‍ $\dbinom{P_0}{P_1}$‍,‍ $\dbinom{P_2}{P_1}$‍,‍ $\dbinom{P_2}{P_3}$‍,‍ $\dbinom{P_4}{P_3}$‍,‍ $\dbinom{P_3}{P_5}$‍‍ и т. д.

Докажем, что с некоторого момента $t$‍‍ перекрашивания в «удвоенной» системе прекратятся, т. е. во все моменты времени, начиная с $t$‍,‍ раскраска «удвоенной» системы приобретёт вид $\dbinom{P_t}{P_{t-1}}$‍‍ или $\dbinom{P_{t-1}}{P_t}$‍.‍ Для исходной системы это будет означать, что её последовательность раскрасок, начиная с некоторого момента, примет вид $\ldots$‍,‍ $P_{t-1}$‍,‍ $P_{t}$‍,‍ $P_{t-1}$‍,‍ $P_{t}$‍,‍ $\ldots$‍‍ (рис. 3), а именно это и требуется доказать в задаче.

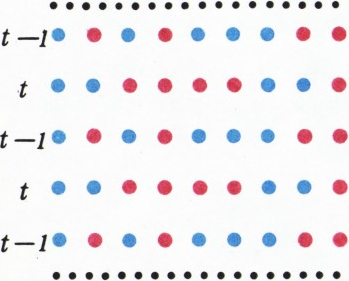
Назовём отрезок $X_i'X_j''$‍,‍ соединяющий точки удвоенной системы, пёстрым ребром, если его концы $X_i'$‍‍ и $X_i''$‍‍ разного цвета. Покажем, что если в очередной момент хотя бы одна точка перекрашивается, то число пёстрых рёбер уменьшается.

Рассмотрим, для определённости, чётный момент времени (точки нижнего ряда не перекрашиваются). Посмотрим на группу рёбер с концом $X_i'$‍.‍ Если в данный момент точка $X_i'$‍‍ нe перекрашивается, то число пёстрых рёбер в этой группе остаётся прежним; если же $X_i'$‍‍ меняет цвет, то, поскольку она приобретает цвет большинства своих соседей, число пёстрых рёбер в этой группе, а следовательно, и их общее число уменьшаются.

Поскольку количество пёстрых рёбер не может уменьшаться бесконечно, с некоторого момента перекрашивания в удвоенной системе прекратятся. Если при этом оба ряда удвоенной системы точек окажутся раскрашенными одинаково, то точки исходной системы перекрашиваться перестанут; если же верхний и нижний ряды удвоенной системы окажутся раскрашенными по-разному, то в исходной системе будут чередоваться две раскраски.

б) Утверждение задачи останется верным. Для доказательства достаточно присоединить к рёбрам удвоенной системы вертикальные отрезки $X_i'X_i''$‍,‍ причём только для таких номеров $i$‍,‍ что точки исходной системы имеют чётное число соседей, после чего дословно повторить проведённые рассуждения.