Задача М654‍‍

Это утверждение неверно. Вот пример шестёрки чисел, среди которых никакие три не имеют общего делителя (большего 1) и нет трёх попарно взаимно простых: 70, 165, 247, 286, 323, 357; ещё один пример, с меньшими числами: 14, 15, 18, 33, 55, 63. Покажем, как строить подобные примеры.

Изобразим наши числа шестью точками; те, у которых есть общий множитель, соединим «ребром» (дугой) и напишем на ребре этот общий множитель. При этом нужно, чтобы все написанные множители были взаимно просты — скажем, это могут быть различные простые числа (иначе три из наших чисел будут иметь общий множитель) — и, кроме того, чтобы из каждых трёх точек по крайней мере две были соединены ребром (иначе найдутся три попарно взаимно простых числа). Построить такой граф — соединить шесть точек рёбрами так, чтобы выполнялось последнее условие — нетрудно; для этого вовсе не обязательно проводить все 15 рёбер между шестью точками — можно обойтись восемью или даже шестью ребрами (рисунки a), б) соответствуют двум приведённым выше примерам); остаётся перемножить числа на всех ребрах, подходящих к каждой из шести вершин, — и пример готов.

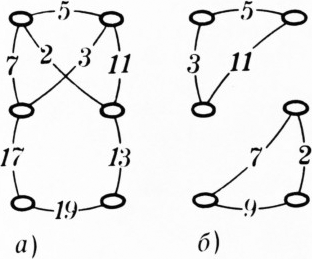
Некоторые читатели ошиблись в решении этой задачи, сославшись на такой факт (мы приводим его в формулировке, предлагавшейся на одной из старых венгерских олимпиад и с тех пор ставшей классической): из шести людей можно выбрать трёх попарно знакомых или трёх попарно незнакомых. Этот факт верен, но дело в том, что три целых числа, попарно имеющих общий множитель, не обязаны иметь общий для всех множитель (больший 1).