Задача М653‍‍‍

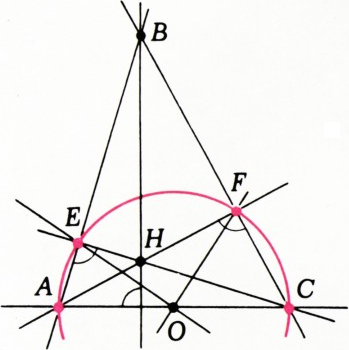
Будем считать длину данного отрезка между отметками равной 1.

а) Проведём две пересекающиеся прямые и отложим на них от точки их пересечения $O$‍‍ отрезки $OA$‍,‍ $OB$‍,‍ $OC$‍,‍ $OD$‍‍ длины 1. Тогда все углы четырёхугольника $ABCD$‍‍ будут прямыми (каждый из них опирается на диаметр $AC$‍‍ или $BD$‍‍ окружности радиуса 1 с центром $O$‍).‍

б) Отложим на данной прямой от точки $O$‍‍ отрезки $OA$‍‍ и $OC$‍‍ длины 1. Затем на каких-нибудь прямых, проходящих через $O$‍,‍ отложим в одной полуплоскости отрезки $OE$‍‍ и $OF$‍‍ длины 1 (см. рисунок). Проведём теперь прямые $AE$‍‍ и $CF$‍,‍ пересекающиеся в некоторой точке $B$‍,‍ и прямые $AF$‍‍ и $CE$‍,‍ пересекающиеся в некоторой точке $H$‍.‍ Тогда прямая $BH$‍‍ будет перпендикулярна данной прямой, поскольку три высоты треугольника всегда пересекаются в одной точке (точки $E$‍‍ и $F$‍‍ служат вершинами прямых углов, опирающихся на диаметр $AC$‍‍ окружности радиуса 1 с центром $O$‍).‍

Теория геометрических построений линейкой и эталоном длины подробно обсуждается в знаменитой книге Д. Гильберта «Основания геометрии» (М.: Гостехиздат, 1948) в связи с анализом системы аксиом. Этими инструментами решаются многие задачи на построение (в частности, через данную точку можно провести прямую, параллельную данной; от данной прямой можно отложить угол, конгруэнтный данному), но, оказывается, не все те задачи, которые разрешимы с помощью циркуля и линейки.