Задача М643‍‍

Приведём два решения этой задачи.

Первое решение. Будем считать, что карточки в стопке расположены в произвольном порядке. Докажем, что за пять перемешиваний их можно упорядочить, а за четыре — не всегда. Тем самым задача будет решена.

Назовём отрезком группу лежащих подряд карточек, номера которых возрастают при удалении от верха стопки. Длиной отрезка будем называть количество входящих в него карточек.

Если имеются два отрезка, то всегда можно, не меняя порядка следования карточек в каждом из них, перемешиванием ниже получить отрезок, состоящий из карточек этих отрезков и только из них. Будем говорить, что такой отрезок получен операцией слияния двух отрезков. Понятно, что длина результата слияния равна сумме длин сливаемых отрезков.

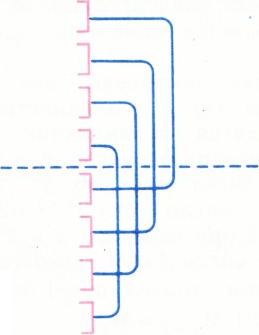
Отметим сначала в стопке карточек 32 отрезка единичной длины и затем будем проделывать перемешивания так:

1. разделим стопку пополам;
2. сливаем попарно отмеченные отрезки соответственно на первой и второй половине стопки;
3. отметим отрезки, получившиеся в результате слияний пункта 2).

Эту операцию повторим пять раз (на рисунке 1 изображено, что происходит с отрезками, получившимися после второго слияния). Длины отрезков, отмеченных до перемешивания, не меньше длин отрезков, отмеченных после него (см. рис. 1). Следовательно, после пяти таких операций длина (единственного!) отмеченного отрезка будет равна $2^5=32$‍.‍ Это доказывает утверждения а) и б) задачи (для пункта а) нужные перемешивания приведены на полях).

Для доказательства того, что произвольное расположение карточки нельзя упорядочить за 4 перемешивания, введём ещё одно понятие. Назовём две соседние в стопке карточки дефектной парой, если карточка с большим номером находится выше карточки с меньшим номером.

Лемма. Если в стопке $n$‍‍ дефектных пар, то после перемешивания в ней будет не менее чем $m=\left[\dfrac n2\right]$‍‍ дефектных пар.

Доказательство. Разделим стопку на две, получим по крайней мере в одной из стопок не менее, чем $m$‍‍ дефектных пар. Действительно, пусть в одной стопке оказалось $k$‍,‍ а в другой $l$‍‍ дефектных пар. Если предположить, что $k\le m-l$‍‍ и $l \lt m$‍,‍ то $k+l\lt2m-1\le n-1$‍.‍ Однако должно быть $k+l\ge n-1$‍,‍ поскольку при разделении стопки могло «разойтись» не более одной дефектной пары. Значит, либо $k\ge m$‍,‍ либо $l\ge m$‍.‍

Заметим теперь, что если между карточками дефектной пары вставлять любые карточки, то при этом образуется хотя бы одна дефектная пара (убедитесь, что это так для одной вставляемой карточки). Тем самым лемма доказана.

Пусть теперь в стопке более 15 дефектных пар. Применим доказанную лемму четыре раза, получим, что после четырёх перемешиваний в стопке остаётся хотя бы одна дефектная пара.

В связи с доказанной леммой возникает интересная задача: зная количество дефектных пар расположения, определить точно минимальное количество перемешиваний, необходимых для достижения этого расположения из упорядоченной стопки. Оказывается, если $N$‍‍ — количество дефектных пар расположения, то необходимо $[\log_2N]+1$‍‍ перемешиваний.

Второе решение. I. б) Рассмотрим операцию, обратную перемешиванию: из произвольных мест стопки вытаскиваем несколько карточек и кладём их сверху. При этом относительный порядок как среди вытащенных, так и среди оставшихся карточек не меняется. Докажем более общее утверждение: $2^n$‍‍ карточек, расположенных в произвольном порядке, можно упорядочить за $n$‍‍ обратных перемешиваний.

Доказательство проведём по индукции.

Для упорядочения двух карточек ($n=1$‍)‍ достаточно одного обратного перемешивания. Пусть уже доказано, что для упорядочения $2^k$‍‍ карточек достаточно $k$‍‍ обратных перемешиваний. Докажем, что $2^{k+1}$‍‍ карточек всегда можно упорядочить за $k+1$‍‍ обратных перемешиваний.

Рассмотрим какое-то расположение $2^{k+1}$‍‍ карточек в стопке. Стопки карточки с номерами от 1 до $2^k$‍‍ (назовём эту стопку красной) и с номерами от $2^k+1$‍‍ до $2^{k+1}$‍‍ (назовём эту стопку голубой) — с относительным расположением карточек внутри каждой стопки таким же, как в стопке из $2^{k+1}$‍‍ карточек — по предположению индукции можно упорядочить за $k$‍‍ обратных перемешиваний. Обозначим эти перемешивания через $A_1$‍,‍ $A_2$‍,‍ $\ldots$‍,‍ $A_k$‍‍ для красной стопки и $B_1$‍,‍ $B_2$‍,‍ $\ldots$‍,‍ $B_k$‍‍ для голубой.

Произведём теперь $k$‍‍ обратных перемешиваний большой стопки (на $2^{k+1}$‍‍ карточек) следующим образом: при $i$‍‍-м обратном перемешивании вытаскиваем красные карточки, которые должны быть вытащены при перемешивании $A_i$‍,‍ и голубые карточки, которые должны быть вытащены при перемешивании $B_i$‍,‍ после чего кладём и те и другие на верх стопки — одни под другими (разобраться в том, что происходит, вам поможет рисунок 2). После $k$‍‍ таких операций красная и голубая стопки оказываются упорядоченными. Остаётся за последнее, $(k+1)$‍‍-е перемешивание вытащить карточки красной стопки и положить их сверху.

II. Докажем, что если в стопке находится больше $2^n$‍‍ карточек, то за $n$‍‍ перемешиваний их нельзя расположить в обратном порядке — по убыванию номеров.

Доказательство проведём по индукции. При $n=1$‍‍ число карточек в стопке не меньше трёх. Так как при перемешивании мы либо берём сверху не менее двух карточек, либо оставляем не менее двух, после одного перемешивания найдутся две карточки, у которых не изменился относительный порядок.

Пусть утверждение верно при $n=k$‍.‍ Для $n=k+1$‍‍ предположим противное, т. е. предположим, что за $k+1$‍‍ перемешиваний удалось получить обратный порядок в стопке, содержащей больше $2^{k+1}$‍‍ карточек. Посмотрим внимательнее, что происходит.

При первом перемешивании либо снимаются сверху, либо остаются неснятыми по крайней мере $2^k+1$‍‍ карточек, т. е. найдётся стопка из $2^k+1$‍‍ карточек, относительный порядок которой после первого перемешивания не изменился. Но по предположению индукции за оставшиеся $k$‍‍ перемешиваний карточки этой стопки нельзя расположить в обратном порядке. Полученное противоречие доказывает утверждение задачи.