Задача М626‍‍

Поскольку середины сторон выпуклого четырёхугольника являются вершинами параллелограмма, его средние линии (красные отрезки на рисунке) в точке пересечения делятся пополам. Применяя это соображение к образовавшимся четырёхугольникам, получим то же утверждение для их средних линий и т. д., так что каждый из отрезков, соединяющих точки деления на противоположных сторонах данного выпуклого четырёхугольника, оказывается разбитым на восемь равных частей.

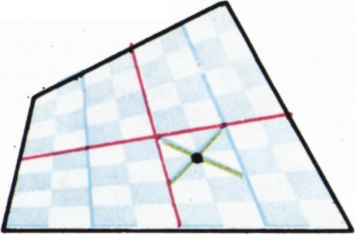
Рассмотрим теперь «удвоенную клетку» разбиения (размером $2\times2$‍;‍ на рисунке в ней выделены зеленым цветом диагонали). То, что суммы площадей синих и белых полей этой удвоенной клетки равны, очевидно (площади соответствующих синих и белых треугольничков с общей вершиной и попарно конгруэнтными основаниями одинаковы). Из этого замечания следует утверждение задачи.