Условие задачи (1980, № 4) Задача М619 // Квант. — 1980. — № 4. — Стр. 30; 1981. — № 2. — Стр. 26.
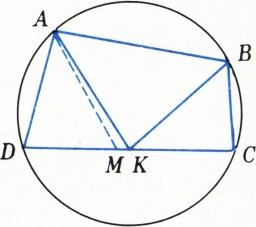
Докажите, что если для вписанного четырёхугольника
Изображения страниц
Решение задачи (1981, № 2) Задача М619 // Квант. — 1980. — № 4. — Стр. 30; 1981. — № 2. — Стр. 26.
Возьмём на стороне