Условие задачи (1979, № 5) Задача М561 // Квант. — 1979. — № 5. — Стр. 22; 1980. — № 3. — Стр. 31—32.
Два треугольника
Изображения страниц
Решение задачи (1980, № 3) Задача М561 // Квант. — 1979. — № 5. — Стр. 22; 1980. — № 3. — Стр. 31—32.
Ответ. Искомая площадь $$ S=\left(\dfrac{\sqrt{S_0}-\sqrt{S_1}}2\right)^2.\tag1 $$
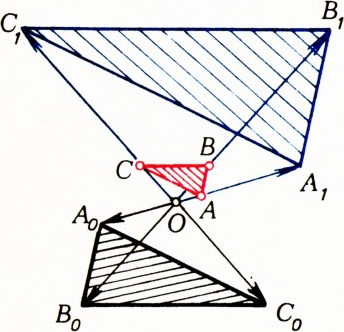
Из условий задачи следует, что треугольники
Пусть
Замечания.
- Треугольники
$A_0B_0C_0$ и$A_1B_1C_1$ могут лежать в параллельных плоскостях; им будет параллельна и плоскость треугольника$ABC$. Все приведённые выше рассуждения и ответ (1) остаются в силе. Наше решение тесно связано с таким полезным фактом: отрезок
$AB$, соединяющий середины диагоналей$A_0A_1$ и$B_0B_1$ трапеции с основаниями$A_0B_0$ и$A_1B_1$, параллелен основаниям и равен по длине полуразности их длин (рис. 2).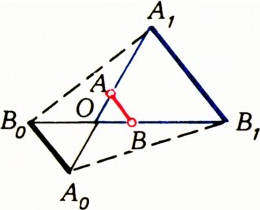
Рис. 2 - Пусть точки
$A_t$, $B_t$, $C_t$ делят отрезки$A_0A_1$, $B_0B_1$, $C_0C_1$ в одном и том же заданном отношении; пусть, например, $$ \overrightarrow{A_0A_t}=t\,\overrightarrow{A_0A_1},\quad \overrightarrow{B_0B_t}=t\,\overrightarrow{B_0B_1},\quad \overrightarrow{C_0C_t}=t\,\overrightarrow{C_0C_1}. $$ Тогда площадь$S_t$ треугольника$A_tB_tC_t$ будет выражаться формулой $$ S_t=(t\sqrt{S_1}-(1-t)\sqrt{S_0})^2,\tag2 $$ обобщающей формулу (1)$\Big($ соответствующую случаю$t=\dfrac12\Big)$. Подумайте, что получается при$t=\dfrac{\sqrt{S_0}}{\sqrt{S_0}+\sqrt{S_1}}$. То обстоятельство, что в задаче даны треугольники, не является существенным; треугольники могут быть заменены другими фигурами, гомотетичными относительно некоторого центра
$O$. Более точно: пусть дана точка$O$ и точка$A_0$ описывает некоторую замкнутую несамопересекающуюся кривую, охватывающую фигуру площади$S_0$ (см. рис. 3). Одновременно точка$A_1$, определяемая вектором$\overrightarrow{OA_1}=-k\,\overrightarrow{OA_0}$, $k=\sqrt{\dfrac{S_1}{S_0}}$, описывает другую кривую (охватывающую фигуру площади$S_1$). Тогда середина$A$ отрезка$A_0A_1$ опишет кривую, охватывающую фигуру площади (1). Аналогично точка$A_t$ такая, что$\overrightarrow{A_0A_t}=t\,\overrightarrow{A_0A_1}$ (т. е.$\overrightarrow{OA_t}=t\,\overrightarrow{OA_0}+(1-t)\overrightarrow{OA_1}= (t-k+kt)\overrightarrow{OA_0}$; $t$ — фиксированное число), опишет кривую, охватывающую фигуру площади, определяемой по формуле (2).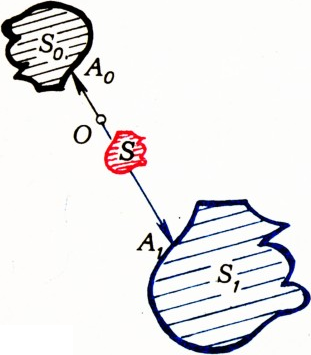
Рис. 3 Интересен следующий факт: в условиях задачи М561 площадь шестиугольника
$KLMNPQ$, где$K$, $L$, $M$, $N$, $P$, $Q$ — середины отрезков$B_0A_1$, $A_1C_0$, $C_0B_1$, $B_1A_0$, $A_0C_1$, $C_1B_0$ соответственно (рис. 4), равна $$ S_{KLMNPQ}=\left(\dfrac{\sqrt{S_0}+\sqrt{S_1}}2\right)^2. $$ (ср. с формулой (1)).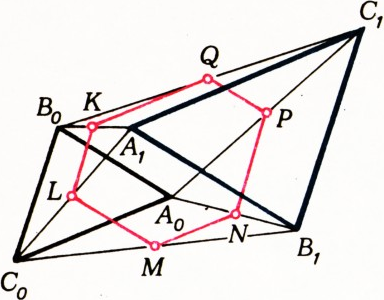
Рис. 4





