Условие задачи (1979, № 3) Задача М551 // Квант. — 1979. — № 3. — Стр. 32; 1980. — № 2. — Стр. 36.
- Какое наименьшее число точек достаточно отметить внутри выпуклого пятиугольника, чтобы внутри любого треугольника с вершинами в вершинах пятиугольника содержалась хотя бы одна отмеченная точка?
- Тот же вопрос для выпуклого
$n$ -угольника.
Изображения страниц
Решение задачи (1980, № 2) Задача М551 // Квант. — 1979. — № 3. — Стр. 32; 1980. — № 2. — Стр. 36.
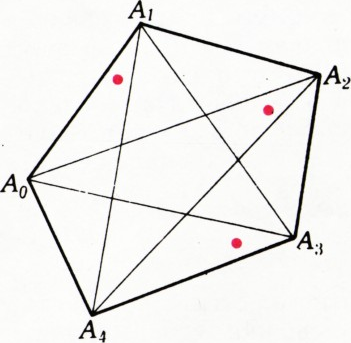
Решим сразу задачу б). Ответ:
Ясно, что необходимо поставить по крайней мере

