Условие задачи (1978, № 12) Задача М539 // Квант. — 1978. — № 12. — Стр. 22; 1979. — № 11. — Стр. 29—31.
Пусть
Изображения страниц
Решение задачи (1979, № 11) Задача М539 // Квант. — 1978. — № 12. — Стр. 22; 1979. — № 11. — Стр. 29—31.
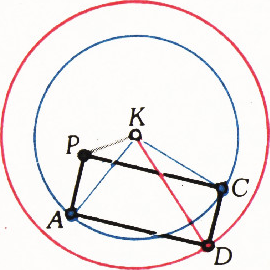
Обсудим сначала аналогичную задачу на плоскости: найти множество четвёртых вершин
- Для любого прямоугольника
$ABCD$ и любой точки$K$ $$ |AK|^2+|CK|^2=|BK|^2+|DK|^2.\tag1 $$
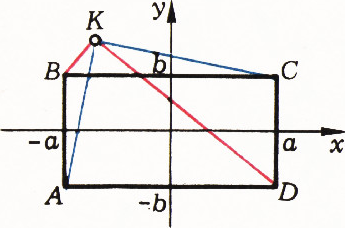
Равенство (1) становится очевидным, если ввести систему координат, как показано на рисунке 5: в обеих частях (1) стоит сумма
$$
(x+a)^2+(y+b)^2+(x-a)^2+(y-b)^2;
$$
здесь
Если
Результат плоского варианта задачи M539 наводит на мысль, что в пространственной задаче ответом будет сфера, концентричная данной. Так оно и есть:
- Все точки
$D$ лежат на сфере с центром в той же точке$K$, что у исходной сферы, и радиусом$\sqrt{3r^2-2p^2}$, где$p=|KP|$, $r$ — радиус исходной сферы.
Это доказали многие читатели, причём самыми разными способами: вычислениями в координатах, с векторами и скалярным произведением и др. Пожалуй, самое простое и наглядное решение получается с помощью той же леммы 1°.
Заметим, что эта лемма верна и для любой точки
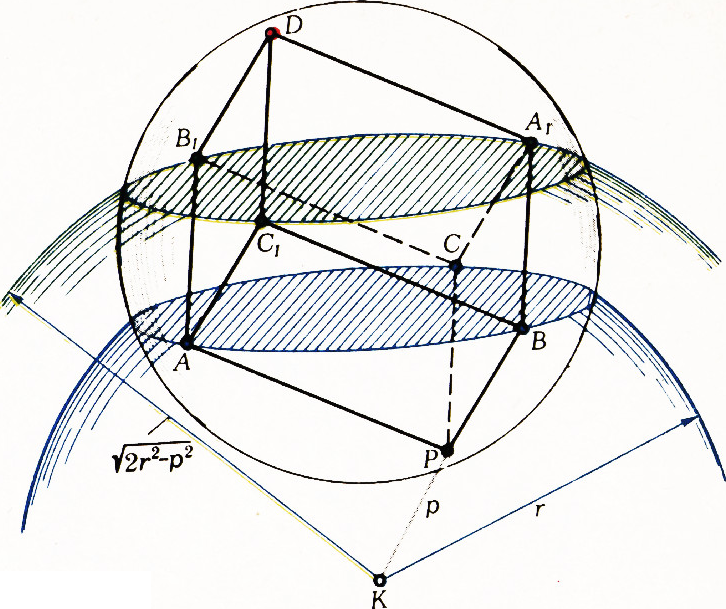
Докажем теперь утверждение 2°. Согласно 1°, вершины
Итак, мы доказали, что вершина
В доказательстве обратного утверждения некоторые читатели использовали метод координат, другие — соображения непрерывности. Мы же и здесь начнём с геометрических наблюдений, которые были сделаны при попытках решить эту задачу:
- Квадраты радиусов четырёх сфер с центром
$K$, на которых лежат точки$P$; $A$, $B$ и$C$; $A_1$, $B_1$ и$C_1$, $D$, образуют арифметическую прогрессию: $$ p^2,\quad r^2,\quad 2r^2-p^2,\quad 3r^2-2p^2. $$
Аналогичная закономерность есть и в плоском варианте (правда, там в прогрессии всего три члена). В связи с этим укажем следующее легко доказываемое утверждение:
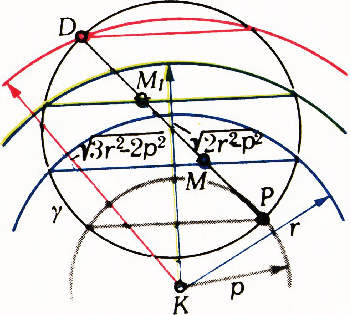
- Если несколько концентрических окружностей, квадраты радиусов которых составляют арифметическую прогрессию, пересекают некоторую окружность
$\gamma$, то общие (с$\gamma$) хорды этих окружностей параллельны и находятся на одинаковом расстоянии друг от друга (рис. 7).
Нам понадобится пространственный вариант этого утверждения, где вместо окружностей фигурируют сферы, вместо хорд — круги и т. п. (он получается из плоского рисунка 7 вращением вокруг оси симметрии).
- Как легко доказать, плоскости
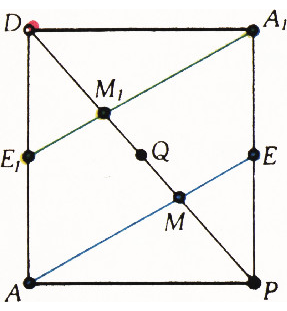
$ABC$ и$A_1B_1C_1$ пересекают диагональ$PD$ параллелепипеда в таких точках$M$ и$M_1$, которые делят её на три одинаковых отрезка:$|PM|=|MM_1|=|M_1D|$ — и являются точками пересечения медиан треугольников$ABC$ и$A_1B_1C_1$ (рис. 8). Середина$Q$ диагонали$PD$ служит центром симметрии параллелепипеда.
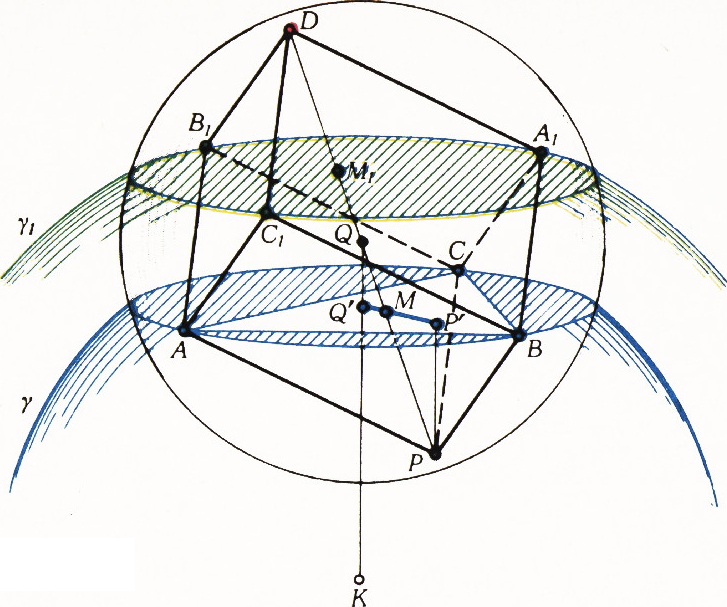
Чтобы получше объяснить пространственные рисунки 6 и 8, укажем ещё следующие факты:
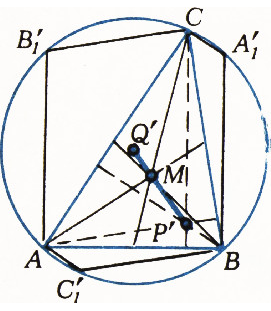
- Проекция
$Q'$ на плоскость$ABC$ центра$Q$ прямоугольного параллелепипеда попадает в центр окружности, описанной вокруг$\triangle ABC$; проекция$P'$ вершины$P$ параллелепипеда — в ортоцентр$\triangle ABC$ (точку пересечения высот).
Отсюда и из 4° легко вывести теорему Эйлера:
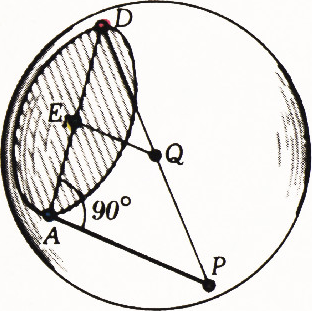
Пусть



